摘要:如图.在平面直角坐标系x0y中.一次函数y=kx+b的图象与反比例函数的图象交于二.四象限内的A.B两点.与x轴交于C点.点B的坐标为(6.n).线段OA=5.E为x轴上一点.且sin∠AOE=. (1)求该反比例函数和一次函数的解析式, (2)求△AOC的面积. 考点:反比例函数综合题. 专题:综合题. 分析:(1)过点A作AD⊥x轴于D点.由sin∠AOE=.OA=5.根据正弦的定义可求出AD.再根据勾股定理得到DO.即得到A点坐标代入y=.确定反比例函数的解析式为y=﹣,将B(6.n)代入.确定点B点坐标.然后把A点和B点坐标代入y=kx+b.求出k和b. (2)先令y=0.求出C点坐标.得到OC的长.然后根据三角形的面积公式计算△AOC的面积即可. 解答:解:(1)过点A作AD⊥x轴于D点.如图. ∵sin∠AOE=.OA=5. ∴sin∠AOE===. ∴AD=4. ∴DO==3. 而点A在第二象限. ∴点A的坐标为. 将A代入y=.得m=﹣12. ∴反比例函数的解析式为y=﹣, 将B(6.n)代入y=﹣.得n=﹣2, 将A分别代入y=kx+b.得 . 解得. ∴所求的一次函数的解析式为y=﹣x+2, (2)在y=﹣x+2中.令y=0. 即﹣x+2=0. 解得x=3. ∴C点坐标为(0.3).即OC=3. ∴S△AOC=•AD•OC=•4•3=6. 点评:本题考查了点的坐标的求法和点在图象上.点的横纵坐标满足图象的解析式,也考查了正弦的定义.勾股定理以及三角形面积公式.
网址:http://m.1010jiajiao.com/timu3_id_435745[举报]
如图,在平面直角坐标系中,点A,B,C,P的坐标分别为(0,2),(3,2),(2,3),(1,1).
(1)请在图中画出△A′B′C′,使得△A′B′C′与△ABC关于点P成中心对称;
(2)若一个二次函数的图象经过(1)中△A′B′C′的三个顶点,求此二次函数的关系式.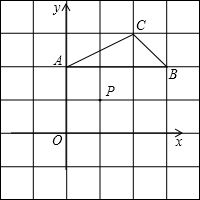 查看习题详情和答案>>
查看习题详情和答案>>
(1)请在图中画出△A′B′C′,使得△A′B′C′与△ABC关于点P成中心对称;
(2)若一个二次函数的图象经过(1)中△A′B′C′的三个顶点,求此二次函数的关系式.
 查看习题详情和答案>>
查看习题详情和答案>>
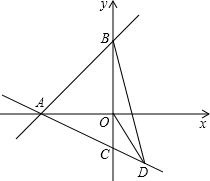
已知:如图,在平面直角坐标系中,0为坐标原点,直线y=x+3与x、y轴分别相交于点A、B,点C在y轴的负半轴上,且∠CAO=30°,点D在线段AC的延长线上,且CD=CO,连接OD、BD,BD交x轴于点E.
(1)求直线AC的解析式;
(2)求证:OB=OD;
(3)图中有几对相似三角形(不添加其他字母和线段)请写出所有的相似三角形,并选择其中的一对加以证明.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求直线AC的解析式;
(2)求证:OB=OD;
(3)图中有几对相似三角形(不添加其他字母和线段)请写出所有的相似三角形,并选择其中的一对加以证明.
 查看习题详情和答案>>
查看习题详情和答案>>
 如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.(1)求tan∠BOA的值;
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;
(3)将△OAB平移得到△O′A′B′,点A的对应点是A′,点B的对应点B'的坐标为(2,-2),在坐标系中作出△O′A′B′,并写出点O′、A′的坐标. 查看习题详情和答案>>
 如图,在平面直角坐标系中,正方形ABCO的点A、C分别在x轴、y轴上,点B坐标为(6,6)连接AC.抛物线y=x2+bx+c经过B、C两点.
如图,在平面直角坐标系中,正方形ABCO的点A、C分别在x轴、y轴上,点B坐标为(6,6)连接AC.抛物线y=x2+bx+c经过B、C两点.(1)求抛物线的解析式.
(2)若动点E从原点出发,以每秒一个单位的速度,沿折线O-C-B-A做匀速运动,同时点F从原点出发,以相同的速度向x正半轴方向做匀速运动,过点E作ED⊥x轴于点D,当点E停止运动时,点F也停止运动.设△EFD的面积为S,运动时间为x(0<x<18),试写出S与x的函数关系式,并求出S的最大值.
(3)P是直线AC上的点,在抛物线上是否存在点Q,使以0、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
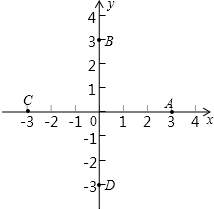 (2013•沙河口区一模)如图,在平面直角坐标系中,坐标是(0,-3)的点是( )
(2013•沙河口区一模)如图,在平面直角坐标系中,坐标是(0,-3)的点是( )