摘要:A.B两所学校在一条东西走向公路的同旁.以公路所在直线为x轴建立如图所示的平面直角坐标系.且点A的坐标是. (1)一辆汽车由西向东行驶.在行驶过程中是否存在一点C.使C点到A.B两校的距离相等.如果有?请用尺规作图找出该点.保留作图痕迹.不求该点坐标. (2)若在公路边建一游乐场P.使游乐场到两校距离之和最小.通过作图在图中找出建游乐场P的位置.并求出它的坐标. 考点:一次函数综合题,线段垂直平分线的性质,作图-应用与设计作图,轴对称-最短路线问题. 专题:综合题. 分析:(1)连接AB.作出线段AB的垂直平分线.与x轴的交点即为所求的点, (2)找到点A关于x轴的对称点.连接对称点与点B与x轴交点即为所求作的点. 解答:解:(1)存在满足条件的点C, 作出图形.如图所示. (2)作点A关于x轴对称的点A′.连接A′B.与x轴的交点即为所求的点P.设A′B所在直线的解析式为:y=kx+b. 把代入得:. 解得:. ∴y=x﹣4. 当y=0时.x=4. 所以交点P为(4.0). 点评:本题是一道典型的一次函数综合题.题目中还涉及到了线段的垂直平分线的性质及轴对称的问题.
网址:http://m.1010jiajiao.com/timu3_id_435720[举报]
A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有?请用尺规作图找出该点,保留作图痕迹,不求该点坐标.
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出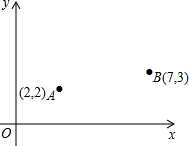 建游乐场P的位置,并求出它的坐标.
查看习题详情和答案>>
建游乐场P的位置,并求出它的坐标.
查看习题详情和答案>>
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有?请用尺规作图找出该点,保留作图痕迹,不求该点坐标.
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出
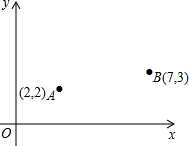 建游乐场P的位置,并求出它的坐标.
查看习题详情和答案>>
建游乐场P的位置,并求出它的坐标.
查看习题详情和答案>>
 A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离之和最小,如果有?请用尺规作图找出该点,保留作图痕迹,并求出它的坐标.
A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离之和最小,如果有?请用尺规作图找出该点,保留作图痕迹,并求出它的坐标.
A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有?请用尺规作图找出该点,保留作图痕迹,不求该点坐标.
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,并求出它的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有?请用尺规作图找出该点,保留作图痕迹,不求该点坐标.
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,并求出它的坐标.
 查看习题详情和答案>>
查看习题详情和答案>>
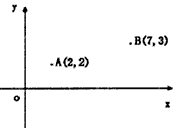
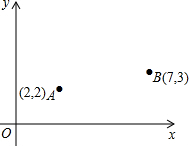 建游乐场P的位置,并求出它的坐标.
建游乐场P的位置,并求出它的坐标.