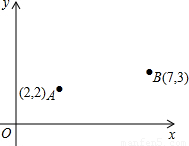题目内容
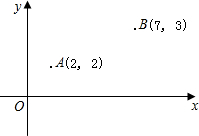 A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离之和最小,如果有?请用尺规作图找出该点,保留作图痕迹,并求出它的坐标.
A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离之和最小,如果有?请用尺规作图找出该点,保留作图痕迹,并求出它的坐标.分析:(1)作A关于x轴的对称点A′,连接A′B即可;
(2)求出A′的坐标,设直线A'B的解析式为y=kx+b,求出直线A′B的解析式,再求出直线与x轴的交点坐标即可.
(2)求出A′的坐标,设直线A'B的解析式为y=kx+b,求出直线A′B的解析式,再求出直线与x轴的交点坐标即可.
解答: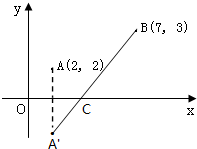 解:(1)如图所示,作A关于x轴的对称点A′,连接A′B交x轴于C,则点C为所求;
解:(1)如图所示,作A关于x轴的对称点A′,连接A′B交x轴于C,则点C为所求;
(2)由图可知,点A'(2,-2),
设直线A'B的解析式为y=kx+b,则有
,
解得
,
∴直线A'B的解析式为y=x-4,
设点C坐标为(a,0),并代入y=x-4,得:
0=a-4,
解得:a=4,
∴点C坐标为(4,0).
 解:(1)如图所示,作A关于x轴的对称点A′,连接A′B交x轴于C,则点C为所求;
解:(1)如图所示,作A关于x轴的对称点A′,连接A′B交x轴于C,则点C为所求;(2)由图可知,点A'(2,-2),
设直线A'B的解析式为y=kx+b,则有
|
解得
|
∴直线A'B的解析式为y=x-4,
设点C坐标为(a,0),并代入y=x-4,得:
0=a-4,
解得:a=4,
∴点C坐标为(4,0).
点评:本题考查了解二元一次方程组,作图与基本作图,用待定系数法求一次函数的解析式,轴对称-最短路线问题等知识点的应用,解(1)小题的关键是理解题意找出C点;解(2)小题的关键是在(1)基础上求出直线A′B的解析式,此题是一道比较好的题目,具有代表性,难度不大.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
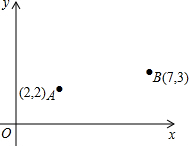 建游乐场P的位置,并求出它的坐标.
建游乐场P的位置,并求出它的坐标. 建游乐场P的位置,并求出它的坐标.
建游乐场P的位置,并求出它的坐标.