摘要:在△ABC中.AB=CB.∠ABC=90°.F为AB延长线上一点.点E在BC上.且AE=CF. (1)求证:Rt△ABE≌Rt△CBF, (2)若∠CAE=30°.求∠ACF的度数. 考点:全等三角形的判定与性质. 专题:几何图形问题,证明题,数形结合. 分析:(1)由AB=CB.∠ABC=90°.AE=CF.即可利用HL证得Rt△ABE≌Rt△CBF, (2)由AB=CB.∠ABC=90°.即可求得∠CAB与∠ACB的度数.即可得∠BAE的度数.又由Rt△ABE≌Rt△CBF.即可求得∠BCF的度数.则由∠ACF=∠BCF+∠ACB即可求得答案. 解答:解:(1)证明:∵∠ABC=90°. ∴∠CBF=∠ABE=90°. 在Rt△ABE和Rt△CBF中.. ∴Rt△ABE≌△Rt△CBF(HL), (2)∵AB=BC.∠ABC=90°. ∴∠CAB=∠ACB=45°. 又∵∠BAE=∠CAB﹣∠CAE=45°﹣30°=15°. 由(1)知:Rt△ABE≌Rt△CBF. ∴∠BCF=∠BAE=15°. ∴∠ACF=∠BCF+∠ACB=45°+15°=60°. 点评:此题考查了直角三角形全等的判定与性质.此题难度不大.解题的关键是注意数形结合思想的应用.
网址:http://m.1010jiajiao.com/timu3_id_435719[举报]
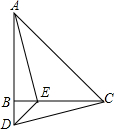 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BCD的度数.
 (2013•芦淞区模拟)在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(2013•芦淞区模拟)在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:BE=BF;
(2)若∠CAE=30°,求∠ACF度数.
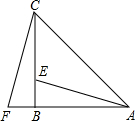 如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.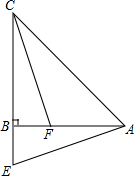 在△ABC中,AB=CB,AB⊥CB,E为CB延长线上一点,点F在AB上,且AE=CF.
在△ABC中,AB=CB,AB⊥CB,E为CB延长线上一点,点F在AB上,且AE=CF.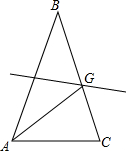 16、如图,在△ABC中,AB=CB=10,底边AC=7,AB的垂直平分线交BC于G,则△AGC的周长为( )
16、如图,在△ABC中,AB=CB=10,底边AC=7,AB的垂直平分线交BC于G,则△AGC的周长为( )