摘要:计箅: (1) (2)解不等式组:.并把解集在数轴上表示出来. (3)先化简.再求值:.其中. 考点:分式的化简求值,零指数幂,负整数指数幂,在数轴上表示不等式的解集,解一元一次不等式组,特殊角的三角函数值. 分析:(1)分别根据负整数指数幂.0指数幂.绝对值及特殊角的三角函数值计算出各数.再根据实数混合运算的法则进行计算即可, (2)分别求出各不等式的解集.再求出其公共解集.并在数轴上表示出来即可, (3)先根据分式混合运算的法则把原式化为最简形式.再把x=代入进行计算即可. 解答:解:(1)原式=3﹣2+2×+1. =3, (2). 由①得.x>﹣2. 由②得.x<4. 故原不等式组的解集为:﹣2<x<4. 在数轴上表示为: (3)原式=÷. =×. =, 当x=时.原式=1﹣=.. 点评:本题考查的是负整数幂.0指数幂及特殊角的三角函数值.解一元一次不等式组.熟知运算的性质是解答此题的关键.
网址:http://m.1010jiajiao.com/timu3_id_435718[举报]
计箅:
(1)(
)-1-|-2|+2sin30°+(
-
)0
(2)解不等式组:
,并把解集在数轴上表示出来.
(3)先化简,再求值:
÷(
-1),其中x=
.
查看习题详情和答案>>
(1)(
| 1 |
| 3 |
| 3 |
| 2 |
(2)解不等式组:
|
(3)先化简,再求值:
| x2-1 |
| x+2 |
| 1 |
| x+2 |
| 1 |
| 3 |
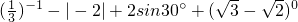
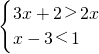 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.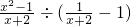 ,其中
,其中 .
.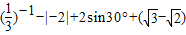
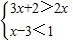 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.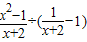 ,其中
,其中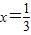 .
.
 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
