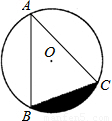
摘要:如图.点A.B.C在直径为2的⊙O上.∠BAC=45°.则图中阴影部分的面积等于.. 考点:扇形面积的计算,圆周角定理. 专题:几何图形问题,数形结合. 分析:首先连接OB.OC.即可求得∠BOC=90°.然后求得扇形OBC的面积与△OBC的面积.求其差即是图中阴影部分的面积. 解答:解:连接OB.OC. ∵∠BAC=45°. ∴∠BOC=90°. ∵⊙O的直径为2. ∴OB=OC=. ∴S扇形OBC==π.S△OBC=××=. ∴S阴影=S扇形OBC﹣S△OBC=π﹣. 故答案为:π﹣. 点评:此题考查了圆周角的性质.扇形的面积与直角三角形面积得求解方法.此题难度不大.解题的关键是注意数形结合思想的应用.
网址:http://m.1010jiajiao.com/timu3_id_435716[举报]
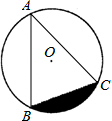 如图,点A、B、C在直径为2
如图,点A、B、C在直径为2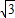 的⊙O上,∠BAC=45°,则图中阴影部分的面积等于 .(结果中保留π).
的⊙O上,∠BAC=45°,则图中阴影部分的面积等于 .(结果中保留π).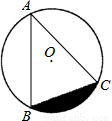
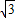 的⊙O上,∠BAC=45°,则图中阴影部分的面积等于 .(结果中保留π).
的⊙O上,∠BAC=45°,则图中阴影部分的面积等于 .(结果中保留π).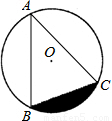
 的⊙O上,∠BAC=45°,则图中阴影部分的面积等于 .(结果中保留π).
的⊙O上,∠BAC=45°,则图中阴影部分的面积等于 .(结果中保留π).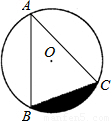
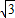 的⊙O上,∠BAC=45°,则图中阴影部分的面积等于 .(结果中保留π).
的⊙O上,∠BAC=45°,则图中阴影部分的面积等于 .(结果中保留π).