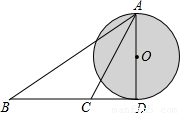
摘要：如图.某小岛受到了污染.污染范围可以大致看成是以点O为圆心.AD长为直径的圆形区域.为了测量受污染的圆形区域的直径.在对应⊙O的切线BD上选择相距300米的B.C两点.分别测得∠ABD=30°.∠ACD=60°.则直径AD= 260 米． (参考数据:.) 考点:解直角三角形的应用. 分析:根据假设CD=x.AC=2x.得出AD=x.再利用解直角三角形求出x的值.进而得出AD的长度． 解答:解:∵∠ABD=30°.∠ACD=60°. ∴假设CD=x.AC=2x. ∴AD=x. tinB==. ∴=. 解得:x=150. ∴∴AD=x=×150≈260米． 故答案为:260米． 点评:此题主要考查了解直角三角形的应用.根据已知假设出CD=x.AC=2x.从而表示出AD.进而利用解直角三角形的知识解决是解决问题的关键．
网址：http://m.1010jiajiao.com/timu3_id_435687[举报]
（2012•平原县一模）如图，某小岛受到了污染，污染范围可以大致看成是以点O为圆心，AD长为直径的圆形区域，为了测量受污染的圆形区域的直径，在对应⊙O的切线BD（点D为切点）上选择相距300米的B、C两点，分别测得∠ABD=30°，∠ACD=60°，则直径AD是多少米？（结果精确到1米）
如图，某小岛受到了污染，污染范围可以大致看成是以点O为圆心，AD长为直径的圆形区域，为了测量受污染的圆形区域的直径，在对应⊙O的切线BD（点D为切点）上选择相距300米的B、C两点，分别测得∠ABD
=30°，∠ACD=60°，则直径AD= 米．（结果精确到1米）
（参考数据：
≈1.414，
≈1.732）
查看习题详情和答案>>
=30°，∠ACD=60°，则直径AD=（参考数据：
| 2 |
| 3 |
（2011•潼南县）如图，某小岛受到了污染，污染范围可以大致看成是以点O为圆心，AD长为直径的圆形区域，为了测量受污染的圆形区域的直径，在对应⊙O的切线BD（点D为切点）上选择相距300米的B、C两点，分别测得∠ABD=30°，∠ACD=60°，则直径AD= 260 米．（结果精确到1米）
（参考数据：
，
）
查看习题详情和答案>>
（参考数据：
，）
查看习题详情和答案>>
，
）
