题目内容
如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD是多少米?(结果精确到1米)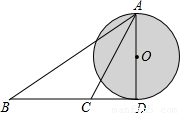
【答案】分析:根据假设CD=x,AC=2x,得出AD= x,再利用解直角三角形求出x的值,进而得出AD的长度.
x,再利用解直角三角形求出x的值,进而得出AD的长度.
解答:解:∵BD是⊙O的切线,
∴∠ADB=90°,
∵∠ABD=30°,∠ACD=60°,
∴设CD=x,则AC=2x,AD=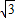 x,
x,
tan∠ABD=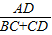 =
=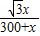 ,
,
∴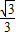 =
= ,
,
解得:x=150,
∴AD=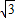 x=
x=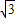 ×150≈260米.
×150≈260米.
答:直径AD长度为260米.
点评:此题主要考查了解直角三角形的应用,根据已知设出CD=x,AC=2x,从而表示出AD,进而利用解直角三角形的知识解决是解决问题的关键.
 x,再利用解直角三角形求出x的值,进而得出AD的长度.
x,再利用解直角三角形求出x的值,进而得出AD的长度.解答:解:∵BD是⊙O的切线,
∴∠ADB=90°,
∵∠ABD=30°,∠ACD=60°,
∴设CD=x,则AC=2x,AD=
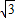 x,
x,tan∠ABD=
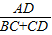 =
=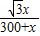 ,
,∴
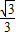 =
= ,
,解得:x=150,
∴AD=
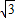 x=
x=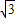 ×150≈260米.
×150≈260米.答:直径AD长度为260米.
点评:此题主要考查了解直角三角形的应用,根据已知设出CD=x,AC=2x,从而表示出AD,进而利用解直角三角形的知识解决是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =30°,∠ACD=60°,则直径AD=
=30°,∠ACD=60°,则直径AD= (2012•平原县一模)如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD是多少米?(结果精确到1米)
(2012•平原县一模)如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD是多少米?(结果精确到1米) ,
, )
)
 ,
, )
)
 ,
, )
)