摘要:如图.在平行四边形ABCD中.直线EF经过其对角线的交点O.且分别交AD.BC于点M.N.交BA.DC的延长线于点E.F.下列结论:①AO=BO,②OE=OF,③△EAM∽△EBN,④△EAO≌△CNO.其中正确的是( ) A.①② B.②③ C.②④ D.③④ 考点:相似三角形的判定与性质,全等三角形的判定与性质,平行四边形的性质. 专题:证明题. 分析:①根据平行四边形的对边相等的性质即可求得AO≠BO.即可求得①错误, ②易证△AOE≌△COF.即可求得EO=FO, ③根据相似三角形的判定即可求得△EAM∽△EBN, ④易证△EAO≌△FCO.而△FCO和△CNO不全等.根据全等三角形的传递性即可判定该选项错误. 解答:解:①平行四边形中邻边垂直则该平行四边形为矩形.故本题中AC≠BD.即AO≠BO.故①错误, ②∵AB∥CD. ∴∠E=∠F. 又∵∠EOA=∠FOC.AO=CO ∴△AOE≌△COF. ∴OE=OF.故②正确, ③∵AD∥BC. ∴△EAM∽△EBN.故③正确, ④∵△AOE≌△COF.且△FCO和△CNO. 故△EAO和△CNO不相似.故④错误. 即②③正确. 故选B. 点评:本题考查了相似三角形的判定.考查了全等三角形对应边相等的性质.考查了平行四边形对边平行的性质.本题中求证△AOE≌△COF是解题的关键.
网址:http://m.1010jiajiao.com/timu3_id_435679[举报]
如图,在平行四边形ABCD中,AB=4,AD=6,∠ABC=60°;点P是射线AD上的一个动点(与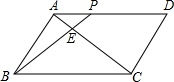 点A不重合),BP与AC相交于点E,设AP=x.
点A不重合),BP与AC相交于点E,设AP=x.
(1)求AC的长;
(2)如果△ABP和△BCE相似,请求出x的值;
(3)当△ABE是等腰三角形时,求x的值. 查看习题详情和答案>>
 点A不重合),BP与AC相交于点E,设AP=x.
点A不重合),BP与AC相交于点E,设AP=x.(1)求AC的长;
(2)如果△ABP和△BCE相似,请求出x的值;
(3)当△ABE是等腰三角形时,求x的值. 查看习题详情和答案>>
如图,在平行四边形ABCD中,AC、BD交于点O,∠ABC=60°,AB=1,E、F分别是线段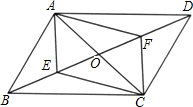 BO、DO上不与点O重合的点,且BE=DF.
BO、DO上不与点O重合的点,且BE=DF.
(1)探究:当BC的长为多少时,四边形AECF是菱形?并说明理由.
(2)当四边形AECF是正方形时,求DF的长. 查看习题详情和答案>>
 BO、DO上不与点O重合的点,且BE=DF.
BO、DO上不与点O重合的点,且BE=DF.(1)探究:当BC的长为多少时,四边形AECF是菱形?并说明理由.
(2)当四边形AECF是正方形时,求DF的长. 查看习题详情和答案>>
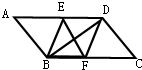 24、如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E.DF平分∠ADC交BC于F.
24、如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E.DF平分∠ADC交BC于F.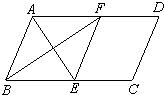 24、如图,在平行四边形ABCD中,∠BAD的平分线与BC边相交于E,∠ABC的平分线与AD边相交于点F.四边形ABEF是什么四边形?试证明你的结论.
24、如图,在平行四边形ABCD中,∠BAD的平分线与BC边相交于E,∠ABC的平分线与AD边相交于点F.四边形ABEF是什么四边形?试证明你的结论.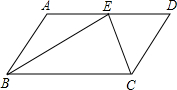 如图,在平行四边形ABCD中,BE、CE分别平分∠ABC,∠BCD,E在AD上,BE=24,CE=7,则平行四边形的周长为
如图,在平行四边形ABCD中,BE、CE分别平分∠ABC,∠BCD,E在AD上,BE=24,CE=7,则平行四边形的周长为