摘要：17．在做“探究单摆周期与摆长的关系 的实验中.如果已知摆球直径为2.00厘米.让刻度尺的零点对准摆线的悬点.摆线竖直下垂.如下图3所示.那么单摆摆长是 .如果测定了50次全振动的时间如下图4中秒表所示.那么秒表读数是 秒.单摆的摆动周期是 秒.
网址：http://m.1010jiajiao.com/timu3_id_1629290[举报]
在做“探究单摆周期与摆长的关系”的实验时，（1）摆球的密度应选得
大
大
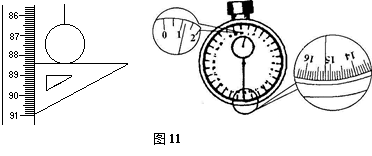
些（填“大”或“小”），如果已知摆球直径为2.00cm，让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如图1所示，那么单摆摆长是0.8740
0.8740
m．如果测定了40次全振动的时间如图2中秒表所示，那么秒表读数是75.2
75.2
s，单摆的摆动周期是1.88
1.88
s．（2）某小组改变摆线长度l0，测量了多组数据．在进行数据处理时，甲同学把摆线长l0作为摆长，直接利用公式求出各组重力加速度值再求出平均值；乙同学作出T2-l0图象后求出斜率，然后算出重力加速度．两同学处理数据的方法对结果的影响是：甲
偏小
偏小
，乙无影响
无影响
（填“偏大”、“偏小”或“无影响”）在做“探究单摆周期与摆长的关系”的实验时，用游标卡尺测量摆球直径如图1所示；让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如图2所示，
（1）那么摆球直径为 mm
（2）单摆摆长是 m（保留四位有效数字）
（3）如果测定了若干次全振动的时间如图3秒表所示，那么秒表读数是 s．
（4）某同学用该实验装置测当地重力加速度，若他测得的g值偏大，可能的原因是 ．
A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时时，秒表过迟按下
D．实验中误将50次全振动数为49次
（5）为提高实验精度，在实验中可改变几次摆长L并测出相应的周期T，从而得出一组对应的L与T的数据，再以L为横坐标、T2为纵坐标将所得数据拟合成直线，并求得该直线的斜率K．则重力加速度g= ．（用K及常数π表示）
查看习题详情和答案>>
（1）那么摆球直径为
（2）单摆摆长是
（3）如果测定了若干次全振动的时间如图3秒表所示，那么秒表读数是
（4）某同学用该实验装置测当地重力加速度，若他测得的g值偏大，可能的原因是
A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时时，秒表过迟按下
D．实验中误将50次全振动数为49次
（5）为提高实验精度，在实验中可改变几次摆长L并测出相应的周期T，从而得出一组对应的L与T的数据，再以L为横坐标、T2为纵坐标将所得数据拟合成直线，并求得该直线的斜率K．则重力加速度g=
在做“探究单摆周期与摆长的关系”的实验时，如果已知摆球直径为2.00cm，让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如图1所示，
（1）那么单摆摆长是 m．
（2）如果测定了40次全振动的时间如图2中秒表所示，那么秒表读数是 s，单摆的摆动周期是 s．
（3）某同学用该实验装置测当地重力加速度，若他测得的g值偏大，可能的原因是
A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时时，秒表过迟按下
D．实验中误将50次全振动数为49次
（4）为提高实验精度，在实验中可改变几次摆长L并测出相应的周期T，从而得出一组对应的L与T的数据，再以L为横坐标、T2为纵坐标将所得数据连成直线，并求得该直线的斜率K．则重力加速度g= ．（用K及常数π表示）
查看习题详情和答案>>
（1）那么单摆摆长是
（2）如果测定了40次全振动的时间如图2中秒表所示，那么秒表读数是
（3）某同学用该实验装置测当地重力加速度，若他测得的g值偏大，可能的原因是A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时时，秒表过迟按下
D．实验中误将50次全振动数为49次
（4）为提高实验精度，在实验中可改变几次摆长L并测出相应的周期T，从而得出一组对应的L与T的数据，再以L为横坐标、T2为纵坐标将所得数据连成直线，并求得该直线的斜率K．则重力加速度g=
