摘要:18.如图所示.电子质量为m.电荷量为e.以速度V0与x轴成θ角射入磁感应强度为B的匀强磁场中扬中.最后落在x轴上的P点.试求: (1)OP间的距离. (2)电子由O点射入.落到P点所需时间t. 19.矩形线框abcd放在磁感应强度为B的匀强磁场中.其匝数为N.面积为S.总电阻为R.t=0时刻开始绕轴OO′以角速度ω匀速转动.如图A.B.C.则: (1)三种情景中能产生变电流的是哪个?并写出相应的电动势的瞬时值表达式. (2)求转动过程中.线圈产生的热量及流过导线某一横截面的电量. 20.如图所示.磁感应强度B = 0.5T的匀强磁场中.垂直于磁场方向水平放置着两根相距h = 0.1m的平行金属导轨MN与PQ导轨电阻忽略不计.两根导轨的端点NQ之间连接一阻值R = 0.3Ω的电阻.导轨上跨放着一根长L = 0.2m.每米长的电阻为r = 2.0Ω的金属棒ab.金属棒与导轨正交放置.交点为c.d.当金属棒以V=4. 0m/s的速度向左做匀速运动时.试求: (1)电阻R中的电流大小和方向, (2)使金属棒匀速运动的外力, (3)金属棒ab两端点间的电势差.21.如图所示.固定的水平光滑金属导轨间距为L.左端接有阻值为R的电阻处在方向竖直.磁感应强度为B的匀强磁场中.质量为m的导体校棒与固定弹簧相连.放在导轨上.导轨与导体棒的电阻可忽略.初始时刻.弹簧恰处于自然长度.导体棒具有水平向右的初速度V0.在沿导轨往复运动的过程中.导体棒始终与导轨垂直并保持良好接触. (1)求初始时刻导体棒受到的安培力, (2)若导体棒从初始时刻到速度第一次为零时.弹簧的弹性势能为EP.则这一过程中安培力所做的功W1和电阻R上产生的焦耳热Q1分虽为多少? (3)导体棒往复运动.最终将静止于何处?从导体棒开始运动直到最终静止的过程中.电阻R上产生的焦耳热Q为多少?
网址:http://m.1010jiajiao.com/timu3_id_1614972[举报]
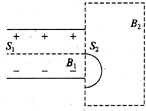 如图所示,一个质量为m,电荷量为q的带负电的粒子(重力不计),以初速度v由狭缝S1,垂直进入电场强度为E的匀强电场中.
如图所示,一个质量为m,电荷量为q的带负电的粒子(重力不计),以初速度v由狭缝S1,垂直进入电场强度为E的匀强电场中.(1)为了使此粒子不改变方向从狭缝S2穿出,则必须在匀强电场区域加入匀强磁场,求匀强磁场B1的大小和方向.
(2)带电粒子从S2穿出后垂直边界进入一个矩形区域,该区域存在垂直纸面向里的匀强磁场,粒子运动轨迹如图所示,若射入点与射出点间的距离为L,求该区域的磁感应强度B2的大小.
 如图所示,一个质量为m,电荷量为e的质子从O点以速度v0垂直NP板射入两板之间区域,两个板间存在垂直纸面向里的匀强磁场,已知两板之间距离为d,板长也为d,O点是NP板的正中间,为使粒子能射出两板间,试求磁感应强度B的大小.
如图所示,一个质量为m,电荷量为e的质子从O点以速度v0垂直NP板射入两板之间区域,两个板间存在垂直纸面向里的匀强磁场,已知两板之间距离为d,板长也为d,O点是NP板的正中间,为使粒子能射出两板间,试求磁感应强度B的大小.如图所示,一个质量为m,电荷量为q的带负电的粒子(重力不计),以初速度v由狭缝S1,垂直进入电场强度为E的匀强电场中.
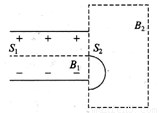
(1)为了使此粒子不改变方向从狭缝S2穿出,则必须在匀强电场区域加入匀强磁场,求匀强磁场B1的大小和方向.
(2)带电粒子从S2穿出后垂直边界进入一个矩形区域,该区域存在垂直纸面向里的匀强磁场,粒子运动轨迹如图所示,若射入点与射出点间的距离为L,求该区域的磁感应强度B2的大小.
查看习题详情和答案>>

