摘要：24．水平放置两块足够长的平行金属板A.B.两板间的距离为0.02m.两板间接入电压为182V的稳压电源.一电子以v0=4×107m/s的速度水平紧靠A板射入电场.如图17所示.电子电量为e=1.6×10-19C.质量m=9.1×10-31kg.试求: (1)电子在电场中的最大水平位移. (2)如果板长为0.4m.那么为了使电子能飞出两板间电场.至少把B向下移动的距离.
网址：http://m.1010jiajiao.com/timu3_id_1611095[举报]
（18分）如图甲所示，两块足够大的平行金属板水平放置，极板间加有空间分布均匀、大小随时间周期性变化、方向竖直向下的电场，变化规律如图乙所示，在t=0时刻从负极板由静止释放一个质量为m、带电量为q（q<0）的质点。已知电场强度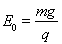
，同时t0也为已知量。
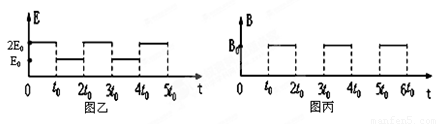
（1）若质点恰好在t=3t0时刻到达正极板，试求两极板之间的距离d
（2）在第（1）问的条件下，在极板间再加上空间分布均匀、大小随时间周期性变化、方向垂直纸面向外的磁场，变化规律如图丙所示，已知磁感应强度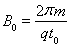
。试求：
①带电质点经过多长时间到达正极板
②带电质点在极板间做圆周运动的最大半径
③画出质点在极板间运动的轨迹图（不需要写计算过程）
查看习题详情和答案>>
（18分）如图甲所示，两块足够大的平行金属板水平放置，极板间加有空间分布均匀、大小随时间周期性变化、方向竖直向下的电场，变化规律如图乙所示，在t=0时刻从负极板由静止释放一个质量为m、带电量为q（q<0）的质点。已知电场强度
，同时t0也为已知量。 
（1）若质点恰好在t=3t0时刻到达正极板，试求两极板之间的距离d
（2）在第（1）问的条件下，在极板间再加上空间分布均匀、大小随时间周期性变化、方向垂直纸面向外的磁场，变化规律如图丙所示，已知磁感应强度
。试求：
①带电质点经过多长时间到达正极板
②带电质点在极板间做圆周运动的最大半径
③画出质点在极板间运动的轨迹图（不需要写计算过程）
（18分）如图甲所示，两块足够大的平行金属板水平放置，极板间加有空间分布均匀、大小随时间周期性变化、方向竖直向下的电场，变化规律如图乙所示，在t=0时刻从负极板由静止释放一个质量为m、带电量为q（q<0）的质点。已知电场强度
，同时t0也为已知量。
（1）若质点恰好在t=3t0时刻到达正极板，试求两极板之间的距离d
（2）在第（1）问的条件下，在极板间再加上空间分布均匀、大小随时间周期性变化、方向垂直纸面向外的磁场，变化规律如图丙所示，已知磁感应强度
。试求：
①带电质点经过多长时间到达正极板
②带电质点在极板间做圆周运动的最大半径
③画出质点在极板间运动的轨迹图（不需要写计算过程）
，同时t0也为已知量。 （1）若质点恰好在t=3t0时刻到达正极板，试求两极板之间的距离d
（2）在第（1）问的条件下，在极板间再加上空间分布均匀、大小随时间周期性变化、方向垂直纸面向外的磁场，变化规律如图丙所示，已知磁感应强度
。试求：①带电质点经过多长时间到达正极板
②带电质点在极板间做圆周运动的最大半径
③画出质点在极板间运动的轨迹图（不需要写计算过程）
两块竖直放置足够长的带电平行金属板A、B，相距d=1.0m，两板间电势差UAB=2500V，O点到两板的距离相等．在O点有一粒子源，释放质量m=2.5×10-3kg、电量q=1.0×10-5C的带正电微粒．过O点以半径R=0.25m作一个圆，圆心O′在过D点向右下方倾斜45°的直线上．M在圆周上．∠OO′M=θ=60°．不计粒子间的相互作用，取g=10m/s2：
（1）求带电微粒在金属板间运动的加速度大小；
（2）若某带电微粒初速度大小为v0=2.0m/s，与水平方向成45°角斜向左上方，试通过计算判断该微粒打在哪个极板上；
（3）若某一微粒在O点射出时初速度方向与水平方向成45°角斜向右上方，且经过一段时间通过M点，求该微粒通过M点时的动能．
查看习题详情和答案>>
（1）求带电微粒在金属板间运动的加速度大小；
（2）若某带电微粒初速度大小为v0=2.0m/s，与水平方向成45°角斜向左上方，试通过计算判断该微粒打在哪个极板上；
（3）若某一微粒在O点射出时初速度方向与水平方向成45°角斜向右上方，且经过一段时间通过M点，求该微粒通过M点时的动能．
如图所示，两块平行金属板M、N竖直放置，板长为L，两板间距为d，且L=d=0.4m，两板间的电势差U=1.0×103V，竖直边界PF、QK之间存在着正交的匀强电场和匀强磁场，其中电场强度E=2.5×103N/C，方向竖直向上；磁感应强度B=1.0×103T，方向垂直纸面向里；C点与N板下端点A在同一水平线上．光滑绝缘斜面CD足够长，倾角为45°，斜面底端与C点重合，现将一电荷量q=+4.0×10-5C的带电小球自M板上边缘由静止释放，沿直线运动到A点后进入叠加场区域，恰好从C点滑上斜面CD．若重力加速度g=10m/s2，求：（1）带电小球的质量．
（2）A点到C点的距离．
（3）带电小球沿斜面CD上滑的最大高度．