在“用单摆测定重力加速度”的实验中：
（1）为了利用单摆较准确地测出重力加速度，可选用的器材为
A．20cm长的结实的细线、小木球、秒表、米尺、铁架台
B．100cm长的结实的细线、小钢球、秒表、米尺、铁架台
C．100cm长的结实的细线、大木球、秒表、50cm量程的刻度尺、铁架台
D．100cm长的结实的细线、大钢球、大挂钟、米尺、铁架台
（2）为了减小测量周期的误差，摆球应在经过最（填“高”或“低”）点的位置时开始计时，并用秒表测量单摆完成多次全振动所用的时间求出周期．
（3）用十分度的游标卡尺测量摆球直径的结果如图所示，则小球的直径为mm．
（4）增大单摆简谐振动周期的方法是．
A．加大摆长  B．加大摆角      C．加大摆球质量D．减小摆球质量
（5）若用L表示摆长，单摆完成20次全振动所用时间为t，那么重力加速度的表达式为g=．

在“用单摆测定重力加速度”的实验中
（1）以下说法正确的是．
A．测量摆长时应将摆球取下后再测量
B．摆球应选用半径约2cm的木球
C．实验中应控制摆角不大于10°是为了减小系统误差
D．实验中只要测量一次全振动的时间即可知道单摆振动的周期
（2）测周期时，当摆球经过位置时开始计时并计数“0”，测出经过该位置100次的时间如图中秒表所示，则周期为．（结果保留3位有效数字）
（3）一组同学在做“用单摆测定重力加速度”的实验，用正确的操作方法，测定了6组摆长L和周期T的对应值．为求出当地的重力加速度，同学们提出了4种不同方法．你认为以下4种方法中，不合理的有
A．从测定的6组数据中任意选取1组，用公式g=4π²L/T ²求出g作为测量值
B．求出L的平均值

.

L

和T的平均值

.

T

，用公式g=4π²

.

L

/

.

T

²求出g作为测量值
C．用6组L、T值，用g=4π²L/T²求出6个g，再求这6个g的平均值作为测量值
D．在坐标纸上作出T ²-L图象，从图象中计算出图线斜率K，根据g=4π²/K求出g．

“在用单摆测定重力加速度”的实验中

（1）用摆长为L和周期T计算重力加速度的公式是g=．
（2）如果用10分度的游标卡尺测得的摆球直径如图甲所示，则摆球的直径d=cm；用最小刻度为1mm的刻度尺的零点对准摆线的悬点，测得的摆线长如图乙所示，则单摆的摆长为L=cm；如果测量了40次全振动的时间如图丙所示，则此单摆的振动周期T=s．
（3）由实验数据得出重力加速度g=π²：．

在“用单摆测定重力加速度”的实验中：
（1）摆动时偏角满足的条件是，为了减小测量周期的误差，计时开始时，摆球应是经过最（填“高”或“低’）点的位置，且用秒表测量单摆完成多次全振动所用的时间，求出周期．单摆振动50次所需时间如图，则单摆振动周期为s．
（2）用最小刻度为1mm的刻度尺测摆长，测量情况如图所示．O为悬挂点，球为匀质小球，从图中可知单摆的摆长为m．
（3）若用L表示摆长，T表示周期，那么重力加速度的表达式为g=．
（4）考虑到单摆振动时空气浮力的影响后，学生甲说：“因为空气浮力与摆球重力方向相反，它对球的作用相当于重力加速度变小，因此振动周期变大．”学生乙说：“浮力对摆球的影响好像用一个轻一些的摆球做实验，因此振动周期不变”，这两个学生中．
A．甲的说法正确    B．乙的说法正确    C．两学生的说法都是错误的．

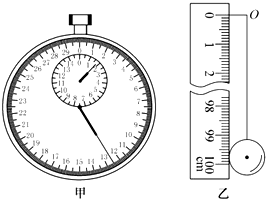在“用单摆测定重力加速度”的实验中：
（1）摆动时偏角α应满足的条件是，为了减小测量周期的误差，计时开始时，摆球应是经过最（填“高”或“低”）点的位置，且用秒表测量单摆完成多次全振动所用的时间，求出周期．图甲中秒表示数为一单摆全振动50次所经过的时间，则单摆振动周期为s． 
（2）用最小刻度为1mm的刻度尺测摆长，测量情况如图乙所示．O为悬挂点，从图乙中可知单摆的摆长为cm．
（3）若用L表示摆长，T表示周期，那么重力加速度的表达式为g=．