摘要：如图18.光滑的平行导轨P.Q间距.处在同一竖直面内.导轨的左端接有如图所示的电路.其中水平放置的电容器两极板相距.定值电阻.导轨的电阻不计.磁感强度的匀强磁场垂直穿过导轨面.当金属棒ab沿导轨向右匀速运动时.电容器两极板之间质量.带电量的微粒恰好静止不动,当S闭合时.微粒以加速度向下做匀加速运动.取.求 (1)金属棒ab运动的速度多大?电阻多大? (2)S闭合后.使金属棒ab做匀速运动的外力的功率多大?
网址：http://m.1010jiajiao.com/timu3_id_1592274[举报]
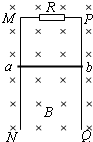如图所示，足够长的光滑平行金属导轨MN、PQ竖直放置，磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面，导轨的上端M与P间连接阻值为R=0.50Ω的电阻，导轨宽度L=0.40m．金属棒ab紧贴在导轨上，现使金属棒ab由静止开始下滑，通过传感器记录金属棒ab下滑的距离h与时间t的关系如下表所示．（金属棒ab和导轨电阻不计，g=10m/s2）| 时 间t/s | 0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 |
| 下滑距离h/m | 0 | 0.18 | 0.60 | 1.20 | 1.95 | 2.80 | 3.80 | 4.80 | 5.80 | 6.80 |
（2）金属棒的质量m；
（3）在前1.60s的时间内，电阻R上产生的热量QR．
如图所示，足够长的光滑平行金属导轨MN、PQ竖直放置，磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面，导轨的上端M与P间连接阻值为R=0.50Ω的电阻，导轨宽度L=0.40m．金属棒ab紧贴在导轨上，现使金属棒ab由静止开始下滑，通过传感器记录金属棒ab下滑的距离h与时间t的关系如下表所示．（金属棒ab和导轨电阻不计，g=10m/s2）
求：（1）在前0.4s的时间内，流过金属棒ab中的电荷量q；
（2）金属棒的质量m；
（3）在前1.60s的时间内，电阻R上产生的热量QR．
查看习题详情和答案>>
| 时 间t/s | 0 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 | 1.60 | 1.80 |
| 下滑距离h/m | 0 | 0.18 | 0.60 | 1.20 | 1.95 | 2.80 | 3.80 | 4.80 | 5.80 | 6.80 |
（2）金属棒的质量m；
（3）在前1.60s的时间内，电阻R上产生的热量QR．
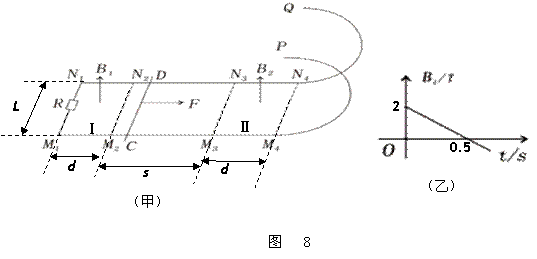
如图8（甲）所示，
、
为平行放置的水平金属轨道，
、
为相同半径，平行放置的竖直半圆形金属轨道,
为切点，P、Q为半圆轨道的最高点，轨道间距
，圆轨道半径
，整个装置左端接有阻值
的定值电阻。M1M2N2N1、M3M4N4N3为等大的长方形区域Ⅰ、Ⅱ，两区域宽度
，两区域之间的距离
；区域Ⅰ内分布着均匀的变化的磁场B1，变化规律如图18（乙）所示，规定竖直向上为B1的正方向；区域Ⅱ内分布着匀强磁场B2，方向竖直向上。两磁场间的轨道与导体棒CD间的动摩擦因数为
，
右侧的直轨道及半圆形轨道均光滑。质量
，电阻
的导体棒CD在垂直于棒的水平恒力F拉动下，从
处由静止开始运动，到达处撤去恒力F，CD棒可匀速地穿过匀强磁场区，并能通过半圆形轨道的最高点PQ处，最后下落在轨道上的位置离
的距离
。若轨道电阻、空气阻力不计，运动过程导棒与轨道接触良好且始终与轨道垂直，g取10 m/s2 求：
（1）水平恒力F的大小；
（2）CD棒在直轨道上运动过程中电阻R上产生的热量Q；
（3）磁感应强度B2的大小。
 |
查看习题详情和答案>>