摘要:如图10-1所示.劲度系数为 K的轻质弹簧一端与墙固定.另一端与倾角为θ的斜面体小车连接.小车置于光滑水平面上.在小车上叠放一个物体.已知小车质量为 M.物体质量为m.小车位于O点时.整个系统处于平衡状态.现将小车从O点拉到B点.令OB=b.无初速释放后.小车即在水平面B.C间来回运动.而物体和小车之间始终没有相对运动.求: (1)小车运动到B点时的加速度大小和物体所受到的摩擦力大小. (2)b的大小必须满足什么条件.才能使小车和物体一起运动过程中.在某一位置时.物体和小车之间的摩擦力为零. 分析与解: (1)所求的加速度a和摩擦力f是小车在B点时的瞬时值.取M.m和弹簧组成的系统为研究对象.由牛顿第二定律:kb=(M+m)a 所以a=kb/(M+m). 取m为研究对象.在沿斜面方向有:f-mgsinθ=macosθ 所以.f=mgsinθ+mcosθ=m(gsinθ+cosθ) (2)当物体和小车之间的摩擦力的零时.小车的加速度变为a'.小车距O点距离为b'.取m为研究对象.有:mgsinθ=ma'cosθ 取M.m和弹簧组成的系统为研究对象.有:kb'=(M+m)a' 以上述两式联立解得:b'=(M+m)gtgθ 说明:在求解加速度时用整体法.在分析求解m受到的摩擦力时用隔离法.整体法和隔离法两者交互运用是解题中常用的方法.希读者认真掌握. 12.如图11-1所示.一列横波t时刻的图象用实线表示.又经△t=0.2s时的图象用虚线表示.已知波长为2m.则以下说法正确的是: A.若波向右传播.则最大周期是2s. B.若波向左传播.则最大周期是2s. C.若波向左传播.则最小波速是9m/s. D.若波速是19m/s.则传播方向向左. 分析与解: 若向右传播.则传播0.2m的波数为0.2m/2m=0.1. 则.△t= 所以T=△t/ 当n=0时.周期有最大值Tmax=2s.所以A正确. 若向左传播.则在0.2s内传播距离为m=1.8m.传过波数为1.8m/2m=0.9. 则.△t= 所以T=△t/ 当n=0时.周期有最大值Tmax≈0.22S.所以B错. 又:T=λ/V.所以V=λ/T=λ/[0.2//0.2=10 当n=0时.波速最小值为Vmin=9m/s.所以C正确. 当n=1时 V=19m/s.所以D正确. 故本题应选A.C.D. 说明:解决波动问题要注意:由于波动的周期性(每隔一个周期T或每隔一个波长λ)和波的传播方向的双向性.往往出现多解.故要防止用特解来代替通解造成解答的不完整.
网址:http://m.1010jiajiao.com/timu3_id_1548925[举报]
如图10-1所示,劲度系数为 K的轻质弹簧一端与墙固定,另一端与倾角为θ的斜面体小车连接,小车置于光滑水平面上。在小车上叠放一个物体,已知小车质量为 M,物体质量为m,小车位于O点时,整个系统处于平衡状态。现将小车从O点拉到B点,令OB=b,无初速释放后,小车即在水平面B、C间来回运动,而物体和小车之间始终没有相对运动。求:(1)小车运动到B点时的加速度大小和物体所受到的摩擦力大小。(2)b的大小必须满足什么条件,才能使小车和物体一起运动过程中,在某一位置时,物体和小车之间的摩擦力为零。

 劲度系数k=40N/m的轻弹簧,一端拴在竖直墙上,另一端拴物体A,A的质量mA=0.2kg,在A的上表面放有质量mB=0.1kg的物体B,如图所示,已知水平地面光滑,A和B之间的最大静摩擦力Fm=0.2N,若要使A、B两物体一起做简谐运动,则( )
劲度系数k=40N/m的轻弹簧,一端拴在竖直墙上,另一端拴物体A,A的质量mA=0.2kg,在A的上表面放有质量mB=0.1kg的物体B,如图所示,已知水平地面光滑,A和B之间的最大静摩擦力Fm=0.2N,若要使A、B两物体一起做简谐运动,则( )| A、物体向右运动过程中B所受摩擦力不断增大 | B、物体向左运动过程中动能减小,弹簧弹性势能增大 | C、物体加速度增大时,速度也增大 | D、振幅的最大值为1.5×10-2m |
一劲度系数k=800 N/m的轻质弹簧两端分别连接着质量均为12 kg的物体A、B,将他们竖直静止在水平面上,如图所示,现将一竖直向上的变力F作用A上,使A由静止开始向上做匀加速运动,经0.4 s物体B刚要离开地面,求:(设整个过程弹簧都在弹性限度内,取g=10 m/s2)
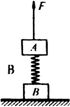
(1)此过程中所加外力F的最大值和最小值;
(2)此过程中力F所做的功
 kx2,x为弹簧的形变量,则此过程中拉力F做的功为多少?
kx2,x为弹簧的形变量,则此过程中拉力F做的功为多少?
