题目内容
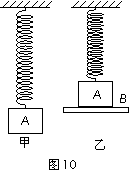
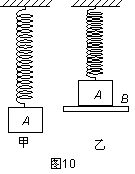
如图10-1所示,劲度系数为 K的轻质弹簧一端与墙固定,另一端与倾角为θ的斜面体小车连接,小车置于光滑水平面上。在小车上叠放一个物体,已知小车质量为 M,物体质量为m,小车位于O点时,整个系统处于平衡状态。现将小车从O点拉到B点,令OB=b,无初速释放后,小车即在水平面B、C间来回运动,而物体和小车之间始终没有相对运动。求:(1)小车运动到B点时的加速度大小和物体所受到的摩擦力大小。(2)b的大小必须满足什么条件,才能使小车和物体一起运动过程中,在某一位置时,物体和小车之间的摩擦力为零。

分析与解:
(1)所求的加速度a和摩擦力f是小车在B点时的瞬时值。取M、m和弹簧组成的系统为研究对象,由牛顿第二定律:kb=(M+m)a 所以a=kb/(M+m)。
取m为研究对象,在沿斜面方向有:f-mgsinθ=macosθ
所以,f=mgsinθ+m![]() cosθ=m(gsinθ+
cosθ=m(gsinθ+![]() cosθ)
cosθ)
(2)当物体和小车之间的摩擦力的零时,小车的加速度变为a’,小车距O点距离为b’,取m为研究对象,有:mgsinθ=ma’cosθ
取M、m和弹簧组成的系统为研究对象,有:kb‘=(M+m)a’
以上述两式联立解得:b‘=![]() (M+m)gtgθ
(M+m)gtgθ
说明:在求解加速度时用整体法,在分析求解m受到的摩擦力时用隔离法。整体法和隔离法两者交互运用是解题中常用的方法,希读者认真掌握。

练习册系列答案
相关题目