摘要:如图㈠-11所示.质量为m=2.0kg的物体静止在水平面上.物体跟水平面间的动摩擦因数为μ=0.20.从t=0时刻起.物体受到一个水平力F的作用而开始运动.前8s内F随时间t变化的规律如图㈠-12所示. 求:⑴在图㈠-13的坐标系中画出物体在前8s内的v-t图象. ⑵前8s内物体所受摩擦力的总冲量If是多大? 17.如图㈠-14所示.光滑斜轨和光滑圆轨相连.固定在同一个竖直面内.圆轨的半径为R.一个小球从离水平面高h处由静止开始自由下滑.由斜轨进入圆轨.⑴为了使小球在圆轨内运动的过程中始终不脱离圆轨.h应在什么范围内取值?⑵若小球到达圆轨最高点时对圆轨的压力大小恰好等于自身重力大小.那么小球开始下滑时的h是多大? 18.如图㈠-15所示.在劲度为k的轻弹簧两端分别固定有两个相同的木块P.Q.质量均为m.开始系统静止在水平桌面上.用竖直向下的力F缓慢向下压P木块到某一位置.系统又处于静止.这时突然撤去压力F.发现P木块开始做简谐运动.而Q木块恰好始终没有离开水平面.求:⑴P做简谐运动的振幅A.⑵振动过程中P的最大加速度am.⑶在缓慢向下压P的过程中压力F所做的功W.19.图㈠-16是塔式起重机的示意图.塔身的竖直中心轴线如图中点划线所示.左右两个支点M.N距中心轴线均为L0=2m.塔自身的重量(不包括配重和被起吊物重量)为G1=5T.重心P距中心轴线d=1m.配重Q的重量为G2=2T.位置固定在距中心轴线L1=6m处.求:⑴不起吊重物时支点N对地面的压力多大?⑵已知起重吊钩R距中心轴线L2=20m.为保证塔吊不倾倒.最大起重重量G是多少吨? 综合测试㈠答案 一.1.B 2.C 3.C 4.D 5.B 6.A 7.C 8.D 二.9.b∶a 10. 11. 12.3.2×105 13.mg(sinα+μcosα)cosα .0 14. 15. 10mv0/3.8mv0/3
网址:http://m.1010jiajiao.com/timu3_id_1547244[举报]
根据经典理论,金属导体中电流的微观表达式为I=nvSe,其中n为金属导体中每单位体积内的自由电子数,v为导体中自由电子沿导体定向移动的速率,S为导体的横截面积,e为自由电子的电荷量.如图11所示,两段长度和材料完全相同、各自粗细均匀的金属导线ab、bc,圆横截面的半径之比为rab∶rbc=1∶4,串联后加上电压U,则 ( )
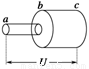
A.两导线内的自由电子定向移动的速率之比为vab∶vbc=1∶4
B.两导线内的自由电子定向移动的速率之比为vab∶vbc=4∶1
C.两导线的电功率之比为Pab∶Pbc=4∶1
D.两导线的电功率之比为Pab∶Pbc=16∶1
查看习题详情和答案>>
如图11所示,将一个质量为1 kg的小物块轻轻放在倾角为37°(sin 37°=0.6)的斜面上,已知斜面质量也为1 kg,重力加速度为10 m/s2。斜面放在足够粗糙的水平地面上没有滑动,那么地面对斜面的支持力FN和摩擦力Ff有可能为( )

图11
A.FN=20 N,Ff=0 N B.FN=20 N,Ff=4.8 N
C.FN=16.4 N,Ff=4.8 N D.FN=16.4 N,Ff=8.5 N
查看习题详情和答案>>根据经典理论,金属导体中电流的微观表达式为I=nvSe,其中n为金属导体中每单位体积内的自由电子数,v为导体中自由电子沿导体定向移动的速率,S为导体的横截面积,e为自由电子的电荷量.如图11所示,两段长度和材料完全相同、各自粗细均匀的金属导线ab、bc,圆横截面的半径之比为rab∶rbc=1∶4,串联后加上电压U,则 ( )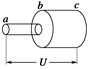
| A.两导线内的自由电子定向移动的速率之比为vab∶vbc=1∶4 |
| B.两导线内的自由电子定向移动的速率之比为vab∶vbc=4∶1 |
| C.两导线的电功率之比为Pab∶Pbc=4∶1 |
| D.两导线的电功率之比为Pab∶Pbc=16∶1 |


