摘要:6.时针和分针转动时:( ) ①分针的角速度是时针的12倍 ②时针的周期是1h.分针的周期是60S ③如果分针的长度是时针的1.5倍,则分针端点的向心加速度是时针端点的216倍 ④如果分针的长度是时针的1.5倍,则分针端点的线速度是时针的18倍 A. ①②③ B. ②③④ C. ①③④ D. ①②④
网址:http://m.1010jiajiao.com/timu3_id_1539822[举报]
手表的时针和分针转动时( )
查看习题详情和答案>>
| A.分针的角速度是时针的12倍 |
| B.时针的周期是12h,分针的周期是60s |
| C.若分针的长度是时针的1.5倍,分针端点的线速度分针是时针的150倍 |
| D.若分针的长度是时针的1.5倍,分针端点的线速度分针是时针的18倍 |
一走时准确的钟表,时针、分针和秒针都做匀速转动,下列关于它们的说法,正确的是( )
A.分针的周期是秒针周期的60倍
B.分针的角速度是秒针角速度的60倍
C.时针的周期是分针周期的24倍
D.时针的角速度是分针角速度的12倍
查看习题详情和答案>>人移动时对绳的拉力不是恒力,重物不是做匀速运动也不是做匀变速运动,故无法用W=Fscosθ求对重物做的功,需从动能定理的角度来分析求解.
当绳下端由A点移到B点时,重物上升的高度为:h=
-H=
重力做功的数值为:WG=
当绳在B点实际水平速度为v时,v可以分解为沿绳斜向下的分速度v1和绕定滑轮逆时针转动的分速度v2,其中沿绳斜向下的分速度v1和重物上升速度的大小是一致的,
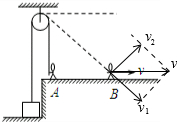
从图中可看出:v1=vcosθ
以重物为研究对象,根据动能定理得:W人-WG=
m
-0
解得:W人=
+
答:在这个过程中,人对重物做的功为
+
.
查看习题详情和答案>>
当绳下端由A点移到B点时,重物上升的高度为:h=
| H |
| sinθ |
| H(1-sinθ) |
| sinθ |
重力做功的数值为:WG=
| mgH(1-sinθ) |
| sinθ |
当绳在B点实际水平速度为v时,v可以分解为沿绳斜向下的分速度v1和绕定滑轮逆时针转动的分速度v2,其中沿绳斜向下的分速度v1和重物上升速度的大小是一致的,

从图中可看出:v1=vcosθ
以重物为研究对象,根据动能定理得:W人-WG=
| 1 |
| 2 |
| v | 21 |
解得:W人=
| mgH(1-sinθ) |
| sinθ |
| mv2cos2θ |
| 2 |
答:在这个过程中,人对重物做的功为
| mgH(1-sinθ) |
| sinθ |
| mv2cos2θ |
| 2 |