摘要：线速度公式: ,角速度公式: ,周期的定义: 根据质点做圆周运动一周的情景.线速度与周期的关系: ,角速度与周期的关系: ,线速度与角速度的关系: .
网址：http://m.1010jiajiao.com/timu3_id_1528213[举报]
根据单摆周期公式可以通过实验测量当地的重力加速度．如图1所示，将细线的上端固定在铁架台上，下端系一个小钢球，就做成了单摆．
①用游标卡尺测量小钢球直径读数如图2所示，则读数为 mm；
②以下是实验过程中的一些做法，其中正确的有 ：
A．摆线要选择细些的、伸缩性小些的，并且尽可能长一些
B．摆球尽量选择质量大些、体积小些的
C．为了使单摆的周期大一些，以方便测量，开始时拉开摆球，使摆线相距平衡位置有较大的角度
D．拉开摆球，使摆线偏离平衡位置较小角度，在释放摆球的同时开始计时，当摆球回到开始位置时停止计时，此时间间隔△t即为单摆周期T
③若测出单摆的周期为T，单摆的摆长为L，则当地的重力加速度g= ．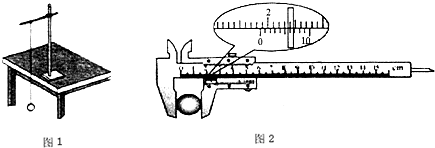
查看习题详情和答案>>
①用游标卡尺测量小钢球直径读数如图2所示，则读数为
②以下是实验过程中的一些做法，其中正确的有
A．摆线要选择细些的、伸缩性小些的，并且尽可能长一些
B．摆球尽量选择质量大些、体积小些的
C．为了使单摆的周期大一些，以方便测量，开始时拉开摆球，使摆线相距平衡位置有较大的角度
D．拉开摆球，使摆线偏离平衡位置较小角度，在释放摆球的同时开始计时，当摆球回到开始位置时停止计时，此时间间隔△t即为单摆周期T
③若测出单摆的周期为T，单摆的摆长为L，则当地的重力加速度g=
在“用单摆测重力加速度”的实验中，（1）某同学的操作步骤为：
a．取一根细线，下端系住直径为d的金属小球，上端固定在铁架台上
b．用米尺量得细线长度l
c．在摆线偏离竖直方向5°位置释放小球
d．用秒表记录小球完成n次全振动的总时间t，得到周期T=
| t |
| n |
e．用公式g=
| 4π2l |
| T2 |
按上述方法得出的重力加速度值与实际值相比
偏小
偏小
（选填“偏大”、“相同”或“偏小”）．（2）已知单摆在任意摆角θ时的周期公式可近似为T′=T0[1+asin2(
| θ |
| 2 |
啊T′（或t、n）、θ
啊T′（或t、n）、θ
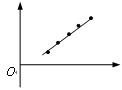
；若某同学在实验中得到了如图甲所示的图线，则图象中的横轴表示| T | ′ |
| T | ′ |
（3）某同学利用如图乙所示的实验装置验证机械能守恒定律，弧形轨道末端水平，离地面的高度为H，将钢球从轨道的不同高度h处静止释放，钢球的落点距轨道末端的水平距离为s．
1）若轨道完全光滑，s2与h的理论关系应满足s2=
4gH
4gH
（用H、h表示）．2）该同学经实验测量得到一组数据，如表所示：
| h（10-1m） | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
| s2（10-1m2） | 2.62 | 3.89 | 5.20 | 6.53 | 7.78 |
3）对比实验结果与理论计算得到的s2-h关系图线（图丙中已画出），自同一高度静止释放的钢球，水平抛出的速率
小于
小于
（填“小于”或“大于”）理论值．4）从s2-h关系图线中分析得出钢球水平抛出的速率差十分显著，你认为造成上述偏差的可能原因是
摩擦、转动（回答任一个即可）
摩擦、转动（回答任一个即可）
．
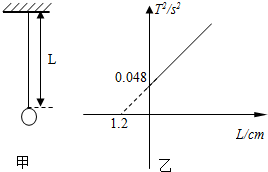在用单摆测重力加速度的实验中：（1）实验时必须控制摆角θ≤
（2）某学生在测量摆长时，只量了悬线的长度L当作摆长，而没有加上摆球的半径，直接将L和测得的周期用单摆的周期公式算出了当地的重力加速度．则测出的重力加速度将比实际的重力加速度
（3）该同学通过改变悬线L长度而测出对应的摆动周期T，再以T2为纵轴、L为横轴画出函数关系图象，实验中所得到的T2-L关系图象如图（乙）所示，由图象可知，摆球的半径r=
在“用单摆测重力加速度”的实验中：
（1）某同学的操作步骤为：
a．取一根细线，下端系住直径为d的金属小球，上端固定在铁架台上；
b．用米尺量得细线长度l；
c．在摆线偏离竖直方向5??位置释放小球；
d．用秒表记录小球完成n次全振动的总时间t，得到周期T=t/n；
e．用公式g=
计算重力加速度。
按上述方法得出的重力加速度与实际值相比 （选填“偏大”、“相同”或“偏小”）。
（2）已知单摆在任意摆角θ时的周期公式可近似为
，式中T0为摆角θ趋近于0??时的周期，a为常数，为了用图像法验证该关系，需要测量的物理量有 ；若某同学在实验中得到了如图所示的图线，则图像中的横轴表示 。
计算重力加速度
，式中T0为摆角趋近于0°时的周期，a为常数。为了用图像法验证该关系式，需要测量的物理量有 ；若某同学在实验中得到了如图所示的图线，则图像中的横轴表示 。