两个带电量均为+q的小球，质量均为m，固定在轻质绝缘等腰直角三角形框架OAB的两个端点A、B上，另一端点用光滑铰链固定在O点，整个装置可以绕垂直于纸面的水平轴在竖直平面内自由转动．直角三角形的直角边长为L．
（1）若施加竖直向上的匀强电场E₁，恰能使框架OB边水平、OA边竖直并保持静止状态，则电场强度E₁多大？在此电场中，框架能否停止在竖直平面内其它位置？
（2）若改变匀强电场的大小和方向（电场仍与框架平行），为使框架的OB边水平，A在O点的正下方，则所需施加匀强电场的场强E₂至少多大？方向如何？
（3）若施加竖直向上的匀强电场E₃=

2mg

q

，小球带电量分别变为q_A=+2q，q_B=+

5

2

q，其余条件不变．将框架从图示位置由静止释放，不计一切摩擦阻力，框架转动多少角度两个小球速度最大？并求出最大速度．

如图甲所示，两个带电小球A、B质量分别为3m、m，电荷量分别为+2q、-q，用一根长为2L的绝缘杆相连，竖直放置，轻杆可绕通过中点O的水平固定转动轴无摩擦转动．现在此空间中施加一个水平向左的匀强电场，电场强度为E，且Eq=mg．在电场力的作用下，整个装置从静止开始转动（带电小球之间的作用力可以忽略不计）求：
（1）轻杆转过90°的过程中，系统电势能的变化量是多少？
（2）当轻杆转过90°时，两个小球的速率是多少？
（3）如果开始时在B小球右侧紧贴放置一个质量为M的光滑绝缘木块，如图乙所示．整个装置重新从竖直位置由静止开始转动，推动木块沿水平面滑动，求转过30°时，绝缘木块的速率是多少？

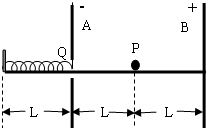如图所示，A、B是两块竖直放置的平行金属板，相距为2L，分别带有等量的负、正电荷，在两板间形成电场强度大小为E的匀强电场．A板上有一小孔（它的存在对两板间匀强电场分布的影响可忽略不计），孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道，一个质量为m，电荷量为g（g＞0）的小球（可视为质点），在外力作用下静止在轨道的中点P处．孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道，轨道上距A板L处有一固定档板，长为L的轻弹簧左端固定在挡板上，右端固定一块轻小的绝缘材料制成的薄板Q．撤去外力释放带电小粒，它将在电场力作用下由静止开始向左运动，穿过小孔后（不与金属板A接触）与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能．小球从接触Q开始，经历时间To第一次把弹簧压缩至最短，然后又被弹簧弹回．由于薄板Q的绝缘性能有所欠缺，使得小球每次离开Q瞬间，小球的电荷量都损失一部分，而变成刚与Q接触时小球电荷量的

1

k

（k＞1）求：
（l）小球第一次接触Q时的速度大小；
（2）假设小球第n次弹回两板间后向右运动的最远处没有到达B板，试导出小球从第n次接触Q，到本次向右运动至最远处的时间Tn的表达式；
（3）若k=2，且小孔右侧的轨道粗糙与带电小球间的滑动摩擦力为f=

qE

4

，试求带电小球最终停止的位置距P点的距离．

如图所示，A和B是两个带有同种电荷小球，电量分别为10^-3c和10^-6c，C是不带电的绝缘木块，B的质量为2Kg，C的质量为3.625Kg，其中A固定在绝缘地面上，B、C恰能悬浮在A的正上方某处，现对C施加一竖直向上的力F，使B、C一起以2.5m/s²加速度竖直向上做匀加速运动．已知静电力常量为k=9×10⁹Nm²/c²，求：
（1）B经过多长时间就要与C脱离．
（2）B在与C脱离前的运动过程中系统电势能减少了4.0625J，求外力F对物体做功为多少？