摘要: 如图2-2-20所示.以两虚线为边界. 中间存在平行纸面且与边界垂直的水平电场.宽度为d.两侧为相同的匀强磁场.方向垂直纸面向里.一质量为m.带电量+q.重力不计的带电粒子.以初速度v1垂直边界射入磁场做匀速圆周运动.后进入电场做匀加速运动.然后第二次进入磁场中运动.此后粒子在电场和磁场中交替运动.已知粒子第二次在磁场中运动的半径是第一次的二倍.第三次是第一次的三倍.以此类推.求: (1)粒子第一次经过电场的过程中电场力所做的功W1. (2)粒子第n次经过电场时电场强度的大小En. (3)粒子第n次经过电场所用的时间tn. (4)假设粒子在磁场中运动时.电场区域场强为零.请画出从粒子第一次射入磁场至第三次离开电场的过程中.电场强度随时间变化的关系图线(不要求写出推导过程.不要求标明坐标刻度值.) 解析:(1)设磁场的磁感应强度大小为B.粒子第n次进入磁场时的半径为Rn.速度为vn.由牛顿第二定律得 qvnB=m ① 由①式得vn= ② 因为R2=2R1.所以v2=2v1 ③ 对于粒子第一次在电场中的运动.由动能定理得 W1=mv-mv ④ 联立③④式得W1=. ⑤ (2)粒子第n次进入电场时速度为vn.出电场时速度为vn+1.有vn=nv1.vn+1=(n+1)v1⑥ 由动能定理得qEnd=mv-mv ⑦ 联立⑥⑦式得En=. ⑧ (3)设粒子第n次在电场中运动的加速度为an.由牛顿第二定律得 qEn=man ⑨ 由运动学公式得vn+1-vn=antn ⑩ 联立⑥⑧⑨⑩式得tn=. 答案:(1)mv (4)如图所示
网址:http://m.1010jiajiao.com/timu3_id_1388981[举报]
(2010?山东模拟)2009年4月15日零时16分,我国在西昌卫星发射中心用“长征三号丙”运载火箭,成功将第二颗北斗导航卫星送入预定轨道.这次发射的北斗导航卫星,是中国北斗卫星导航系统建设计划中的第二颗组网卫星,是地球同步静止轨道卫星.该卫星在预定轨道正常运行时,下列说法中正确的是( )
查看习题详情和答案>>
 (2010?山东)如图所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且垂直纸面,MN、PQ为其边界,OO′为其对称轴一导线折成边长为l的正方形闭合加在路abcd,回路在纸面内以恒定速度v0向右运动,叵运动到关于OO′对称的位置时( )
(2010?山东)如图所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且垂直纸面,MN、PQ为其边界,OO′为其对称轴一导线折成边长为l的正方形闭合加在路abcd,回路在纸面内以恒定速度v0向右运动,叵运动到关于OO′对称的位置时( )
查看习题详情和答案>>
 (2010?山东)一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头( )
(2010?山东)一理想变压器原、副线圈的匝数比为10:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头( )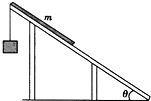 (2010?山东)如图所示,倾角θ=30°的粗糙斜面固定在地面上,长为l,质量为m,粗细均匀,质量分布均匀的软绳置于斜面上,其上端下斜面顶端齐平.用细线将物块与软绳连接,物块由静止释放后向下运动,直到软绳刚好全部离开斜面(此时物块未到达地面),在此过程中( )
(2010?山东)如图所示,倾角θ=30°的粗糙斜面固定在地面上,长为l,质量为m,粗细均匀,质量分布均匀的软绳置于斜面上,其上端下斜面顶端齐平.用细线将物块与软绳连接,物块由静止释放后向下运动,直到软绳刚好全部离开斜面(此时物块未到达地面),在此过程中( )