摘要：13．如图所示.质量为m的滑块.放在光滑的水平平台上.平台右端B与水平传送带相接.传送带的运行速度为v0.长为L.今将滑块缓慢向左压缩固定在平台上的轻弹簧.到达某处时突然释放.当滑块滑到传送带右端C时.恰好与传送带速度相同．滑块与传送带间的动摩擦因数为μ. (1)试分析滑块在传送带上的运动情况, (2)若滑块离开弹簧时的速度大于传送带的速度.求释放滑块时.弹簧具有的弹性势能, (3)若滑块离开弹簧时的速度大于传送带的速度.求滑块在传送带上滑行的整个过程中产生的热量． [答案] (1)见解析 (2)mv+μmgL (3)μmgL-mv0·(-v0) [解析] (1)若滑块冲上传送带时的速度小于带速.则滑块在带上由于受到向右的滑动摩擦力而做匀加速运动,若滑块冲上传送带时的速度大于带速.则滑 块由于受到向左的滑动摩擦力而做匀减速运动． (2)设滑块冲上传送带时的速度为v. 由机械能守恒Ep＝mv2. 设滑块在传送带上做匀减速运动的加速度大小为a. 由牛顿第二定律:μmg＝ma. 由运动学公式v2-v＝2aL. 解得Ep＝mv+μmgL. (3)设滑块在传送带上运动的时间为t.则t时间内传送带的位移x＝v0t.v0＝v-at 滑块相对传送带滑动的位移Δx＝L-x 相对滑动生成的热量Q＝μmg·Δx 解得Q＝μmgL-mv0·(-v0)．
网址：http://m.1010jiajiao.com/timu3_id_1386687[举报]
（2009?天津模拟）如图所示，两根光滑直杆（粗细可忽略不计）水平平行放置，一质量为m、半径为r的均匀细圆环套在两根直杆上，两杆之间的距离为| 3 |
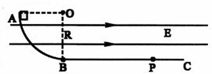（2009?天津模拟）如图所示，竖直面内有一绝缘轨道，AB部分是光滑的四分之一圆弧，圆弧半径R=0.5m，B处切线水平，BC部分为水平粗糙直轨道．有一个带负电的小滑块（可视为质点）从A点由静止开始下滑，运动到直轨道上的P处刚好停住．小滑块的质量m=1kg，带电量为q=-2.5×10-3C保持不变，滑块小轨道BC部分间的动摩擦因数为μ=0.2，整个空间存在水平向右的匀强电场，电场强度大小为E=4.0×102N/C．（g=10m/s2）（1）求滑块到达B点前瞬间对轨道的压力大小．
（2）求BP间的距离．
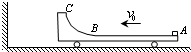（2009?天津模拟）如图所示，小车的质量为M=3kg，车的上表面左端为| 1 | 4 |
（1）小物块沿圆弧上升的最大高度为多少？
（2）小物块从最高点返回后与车的速度相同时，小物块距B端多远．
（2009?天津模拟）如图甲所示，abcd是位于竖直平面内的正方形闭合金属线框，底边bc水平，金属线框的质量为m，电阻为R．在金属线框的下方有一水平方向的匀强磁场区域，MN和M′N′是匀强磁场区域的上下边界，并与线框的bc边平行，磁场方向与线框平面垂直．现金属线框从磁场上方某一高度处由静止开始下落，图乙是金属线框由开始下落到完全穿过磁场区域瞬间的速度-时间图象，图象中坐标轴上所标出的字母均为已知量，重力加速度为g，忽略空气阻力．求：
（2009?天津模拟）如图甲所示，质量为2m的长木板静止地放在光滑的水平面上，另一质量为m的小铅块（可视为质点）以水平速度v0滑上木板的左端，恰能滑至木板的右端且与木板保持相对静止，铅块在运动过程中所受到的摩擦力始终不变．若将木板分成长度与质量均相等（即m1=m2=m）的两段1、2后，将它们紧挨着放在同一水平面上，让小铅块以相同的初速度v0由木板1的左端开始运动，如图乙所示，则下列说法正确的是（ ）