摘要：如图甲所示.两个光滑的斜面高度相同.右边由两部分组成.且AB+BC＝AD.两小球a.b分别从A点沿两侧斜面由静止滑下.不计转折处的能量损失.两次下滑的时间分别为t1与t2.则( ) A.t1＞t2 B.t1＜t2 C.t1＝t2 D.无法判断 解析:由于在下滑的过程中不损失机械能.因此质点到达C点和D点的速度大小均为v.如图乙所示.即两次下滑的速率随时间变化的v-t图象中图线的终点均应落在直线vF上.OF为沿AD下滑的v-t图线.OG为下滑AB段的图线.由于AB段的加速度比AD段的大.故OG的斜率比OF的斜率大.GH为BC段图线.H落在vF上.那么H落在F的左边.右边还是与F重合呢? 若H正好与F重合.那么四边形OGHt1的面积比三角形OFt1的面积大.这说明沿ABC下滑的路程较大.这与AD＝AB+BC相矛盾.所以H不可能与F重合.即t1不可能等于t2. 若H在F的右边.如图丙所示.过H作HI∥OF交t轴于I.则S△HIt2＝S△FOt1.而△HIt2是四边形OGHt2的一部分.故S四边形OGHt2＞S△FOt1.与题设矛盾.所以H只能在F的左边.即t1＞t2.选项A正确. 答案:A
网址：http://m.1010jiajiao.com/timu3_id_1385145[举报]
如图甲所示，两个等量同种电荷固定于光滑水平面上，其连线中垂线上有A、B、C三点，一个电荷量q=2C，质量m=1kg的小物块从C点由静止释放，其仅在电场力作用下运动的v-t图象如图乙所示，其中B点处为整条图线切线斜率最大的位置（图中标出了该切线）．则下列说法正确的是（ ）
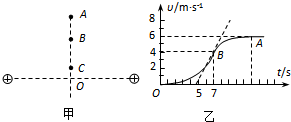
| A、A、B两点的电势差UAB=-5V | B、由C点到A点的过程中，电势逐渐升高 | C、由C点到A点的过程中，物块电势能先减小后变大 | D、B点为中垂线上电场强度最大的点，场强E=2 V/m |
如图甲所示，两个足够长且电阻不计的光滑金属轨道，间距L＝1 m，在左端斜轨道部分高h＝1.25 m处放置一金属杆a，斜轨道与平直轨道区域以光滑圆弧连接，在平直轨道右端放置另一金属杆b，杆a、b的电阻分别为Ra＝2 Ω、Rb＝4 Ω．在平面轨道区域有竖直向上的匀强磁场，磁感应强度B＝2 T，现杆b以初速度v0＝5 m/s开始向左滑动，同时由静止释放杆a．从a下滑到水平轨道时开始计时，a、b杆运动的速度－时间图象如图乙所示．其中ma＝2 kg，mb＝1 kg，g＝10 m/s2，以a的运动方向为正．求：
(1)当杆a在水平轨道上的速度为3 m/s时，杆b的加速度为多少？
(2)在整个运动过程中杆b上产生的焦耳热．
(3)杆a在斜轨道上运动的时间内杆b向左移动的距离．
如图甲所示，甲、乙两个小球可视为质点，甲球沿倾角为30°的光滑足够长斜面由静止开始下滑，乙球做自由落体运动，甲、乙两球的动能与路程的关系图象如图乙所示．下列说法正确的是（ ）| A、甲球机械能不守恒，乙球机械能守恒 | B、甲、乙两球的质量之比为m甲：m乙=4：1 | C、甲、乙两球的动能均为Ek0时，两球重力的瞬时功率之比为P甲：P乙=1：1 | D、甲、乙两球的动能均为Ek0时，两球高度相同 |
如图甲所示，甲、乙两个小球可视为质点，甲球沿倾角为30°的光滑足够长斜面由静止开始下滑，乙球做自由落体运动，甲、乙两球的动能与路程的关系图象如图乙所示．下列说法正确的是（ ）
| A、甲球机械能不守恒，乙球机械能守恒 | B、甲、乙两球的质量之比为m甲：m乙=4：1 | C、甲、乙两球的动能均为Ek0时，两球重力的瞬时功率之比为P甲：P乙=1：1 | D、甲、乙两球的动能均为Ek0时，两球高度相同 |
如图甲所示，甲、乙两个小球可视为质点，甲球沿倾角为30°的光滑足够长斜面由静止开始下滑，乙球做自由落体运动，甲、乙两球的动能与路程的关系图象如图乙所示．下列说法正确的是（ ）
| A、甲球机械能不守恒，乙球机械能守恒 | ||||||
| B、甲、乙两球的质量之比为m甲：m乙=4：1 | ||||||
C、甲、乙两球的动能均为
| ||||||
| D、甲、乙两球的动能均为Ek0时，两球高度相同 |