摘要:如图甲所示.竖直平面上有一光滑绝缘的半圆形轨道.处于水平方向且与轨道平面平行的匀强电场中.轨道两端点A.C高度相同.轨道的半径为R . 一个质量为m的带正电的小球从槽右端的A处无初速度地沿轨道下滑.滑到最低点B时对槽底压力为2mg. 求小球在滑动过程中的最大速度. 甲.乙两位同学是这样求出小球的最大速度的: 甲同学:B是轨道的最低点.小球过B点时速度最大.小球在运动过程中机械能守恒.mgR=mv2.解得小球在滑动过程中的最大速度为v=. 乙同学:B是轨道的最低点.小球过B点时速度最大.小球在B点受到轨道的压力为FN=2 mg.由牛顿第二定律有FN-mg=m.解得球在滑动过程中的最大速度v=. 请分别指出甲.乙同学的分析是否正确.若错误.将最主要的错误指出来.解出正确的答案.并说明电场的方向. 解析:甲同学的分析是错误的.小球的机械能不守恒. 乙同学的分析也是错误的.小球在滑动过程中的最大速度的位置不在最低点B. 正解如下: 小球在B点时.FN-mg=m 而FN=2mg.解得:v2=gR 从A到B.设电场力做功WE.由动能定理.有: WE+mgR=mv2 得WE=-mgR 电场力做负功. 所以带电小球所受电场力的方向向右 FE==mg.场强方向向右 从A到B之间一定有位置D.小球运动至该点时合外力与速度方向垂直.小球在该点速度达到最大.设O.D连线与竖直方向间的夹角为θ.如图乙所示.则有: cos θ==.sin θ= 又由动能定理.有: mv=mgRcos θ-FE(R-Rsin θ) 解得:vmax=. 答案:略
网址:http://m.1010jiajiao.com/timu3_id_1384562[举报]
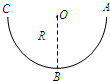 如图所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R.一个质量为m的带正电的小球从槽右端的A处无初速沿轨道下滑,滑到最低点B时对槽底压力为2mg.求小球在滑动过程中的最大速度.
如图所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R.一个质量为m的带正电的小球从槽右端的A处无初速沿轨道下滑,滑到最低点B时对槽底压力为2mg.求小球在滑动过程中的最大速度.两位同学是这样求出小球的最大速度的:
甲同学:B是轨道的最低点,小球过B点时速度最大,小球运动过程机械能守恒,mgR=
| 1 |
| 2 |
| 2gR |
乙同学:B是轨道的最低点,小球过B点时速度最大,小球在B点受到轨道的压力为FN=2mg,由牛顿第二定律有FN-mg=m
| v2 |
| R |
| gR |
请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.
如图所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点 、
、 高度相同,轨道的半径为
高度相同,轨道的半径为 .一个质量为
.一个质量为 的带正电的小球从槽右端的
的带正电的小球从槽右端的 处无初速沿轨道下滑,滑到最低点
处无初速沿轨道下滑,滑到最低点 时对槽底压力为2mg.求小球在滑动过程中的最大速度.?
时对槽底压力为2mg.求小球在滑动过程中的最大速度.?

两位同学是这样求出小球的最大速度的:?
甲同学:![]() 是轨道的最低点,小球过
是轨道的最低点,小球过![]() 点时速度最大,小球运动过程机械能守恒,
点时速度最大,小球运动过程机械能守恒,![]() ,解得小球在滑动过程中的最大速度为
,解得小球在滑动过程中的最大速度为![]() .?
.?
乙同学:![]() 是轨道的最低点,小球过
是轨道的最低点,小球过![]() 点时速度最大,小球在
点时速度最大,小球在![]() 点受到轨道的支持力为
点受到轨道的支持力为![]() ,由牛顿第二定律有
,由牛顿第二定律有![]() ,解得球在滑动过程中的最大速度为
,解得球在滑动过程中的最大速度为![]() .?
.?
请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.
查看习题详情和答案>>如图所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R.一个质量为m的带正电的小球从槽右端的A处无初速沿轨道下滑,滑到最低点B时对槽底压力为2mg.求小球在滑动过程中的最大速度.
两位同学是这样求出小球的最大速度的:
甲同学:B是轨道的最低点,小球过B点时速度最大,小球运动过程机械能守恒,mgR=
mv2,解得小球在滑动过程中的最大速度为v=
.
乙同学:B是轨道的最低点,小球过B点时速度最大,小球在B点受到轨道的压力为FN=2mg,由牛顿第二定律有FN-mg=m
,解得球在滑动过程中的最大速度v=
.
请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.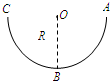
查看习题详情和答案>>
两位同学是这样求出小球的最大速度的:
甲同学:B是轨道的最低点,小球过B点时速度最大,小球运动过程机械能守恒,mgR=
| 1 |
| 2 |
| 2gR |
乙同学:B是轨道的最低点,小球过B点时速度最大,小球在B点受到轨道的压力为FN=2mg,由牛顿第二定律有FN-mg=m
| v2 |
| R |
| gR |
请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.

如图所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点A、C高度相同,轨道的半径为R.一个质量为m的带正电的小球从槽右端的A处无初速沿轨道下滑,滑到最低点B时对槽底压力为2mg.求小球在滑动过程中的最大速度.
两位同学是这样求出小球的最大速度的:
甲同学:B是轨道的最低点,小球过B点时速度最大,小球运动过程机械能守恒, ,解得小球在滑动过程中的最大速度为
,解得小球在滑动过程中的最大速度为 .
.
乙同学:B是轨道的最低点,小球过B点时速度最大,小球在B点受到轨道的压力为FN=2mg,由牛顿第二定律有 ,解得球在滑动过程中的最大速度
,解得球在滑动过程中的最大速度 .
.
请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.
 查看习题详情和答案>>
查看习题详情和答案>>
两位同学是这样求出小球的最大速度的:
甲同学:B是轨道的最低点,小球过B点时速度最大,小球运动过程机械能守恒,
 ,解得小球在滑动过程中的最大速度为
,解得小球在滑动过程中的最大速度为 .
.乙同学:B是轨道的最低点,小球过B点时速度最大,小球在B点受到轨道的压力为FN=2mg,由牛顿第二定律有
 ,解得球在滑动过程中的最大速度
,解得球在滑动过程中的最大速度 .
.请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.
 查看习题详情和答案>>
查看习题详情和答案>>
如图1-5-13 所示,竖直平面上有一光滑绝缘半圆轨道,处于水平方向且与轨道平面平行的匀强电场中,轨道两端点 A、C 高度相同,轨道的半径为 R.一个质量为 m 的带正电的小球从槽右端的 A 处无初速沿轨道下滑,滑到最低点 B 时对槽底压力为 2mg.求小球在滑动过程中的最大速度.

图1-5-13
两位同学是这样求出小球的最大速度的:
甲同学:B 是轨道的最低点,小球过 B 点时速度最大,小球运动过程机械能守恒,mgR=![]() mv2,解得小球在滑动过程中的最大速度为 v=
mv2,解得小球在滑动过程中的最大速度为 v=![]() .
.
乙同学:B 是轨道的最低点,小球过 B 点时速度最大,小球在 B 点受到轨道的支持力为 Fn=2mg,由牛顿第二定律有 Fn-mg=m![]() ,解得球在滑动过程中的最大速度为 v=
,解得球在滑动过程中的最大速度为 v=![]() .
.
请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.
查看习题详情和答案>>