摘要：一飞船在某星球表面附近.受星球引力作用而绕其做匀速圆周运动的速率为v1.飞船在离该星球表面高度为h处.受星球引力作用而绕其做匀速圆周运动的速率为v2.已知引力常量为G. (1)求该星球的质量. (2)若设该星球的质量为M.一个质量为m的物体在离该星球球心r远处具有的引力势能为Ep＝-.则一颗质量为m的卫星由r1轨道变为r2(r1＜r2)轨道.对卫星至少做多少功?(卫星在r1.r2轨道上做匀速圆周运动.结果请用M.m.r1.r2.G表示) 解析:(1)设星球的半径为R.质量为M.由万有引力定律及向心力分公式得: G＝m G＝m 联立解得:M＝. (2)卫星在轨道上的机械能E＝Ek+Ep＝-G 故有W＝E2-E1＝GMm(). 答案:GMm() 第22讲 万有引力定律及其应用Ⅱ 体验成功
网址：http://m.1010jiajiao.com/timu3_id_1384268[举报]
一飞船在某星球表面附近，受星球引力作用而绕其做匀速圆周运动的速率为v1；飞船在离该星球表面高度为h处，受星球引力作用而绕其做匀速圆周运动的速率为v2．已知万有引力恒量为G．试求
（1）该星球的质量
（2）若设该星球的质量为M，一个质量为m的物体在离该星球球心r远处具有的引力势能为EPr=-
，则一颗质量为m1的卫星由r1轨道变为r2（r1＜r2）轨道，对卫星至少做多少功？（卫星在r1、r2轨道上均做匀速圆周运动，结果请用M、m1、r1、r2、G表示）
查看习题详情和答案>>
（1）该星球的质量
（2）若设该星球的质量为M，一个质量为m的物体在离该星球球心r远处具有的引力势能为EPr=-
| GMm | r |
一飞船在某星球表面附近，受星球引力作用而绕其做匀速圆周运动的速率为v1，飞船在离该星球表面高度为h处，受星球引力作用而绕其做匀速圆周运动的速率为v2，已知万有引力常量为G.试求：
(1)该星球的质量；
(2)若设该星球的质量为M，一个质量为m的物体在离该星球球心r远处具有的引力势能为Ep＝－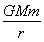
，则一颗质量为m1的卫星由r1轨道变为r2(r1＜r2)轨道，对卫星至少做多少功？(卫星在r1、r2轨道上均做匀速圆周运动，结果请用M、m1、r1、r2、G表示)
查看习题详情和答案>>
一飞船在某星球表面附近，受星球引力作用而绕其做匀速圆周运动的速率为v1，飞船在离该星球表面高度为h处，受星球引力作用而绕其做匀速圆周运动的速率为v2，已知万有引力常量为G.试求：
(1)该星球的质量；
(2)若设该星球的质量为M，一个质量为m的物体在离该星球球心r远处具有的引力势能为Ep＝－
，则一颗质量为m1的卫星由r1轨道变为r2(r1＜r2)轨道，对卫星至少做多少功？(卫星在r1、r2轨道上均做匀速圆周运动，结果请用M、m1、r1、r2、G表示)