摘要：4．如图所示.质量为M=3kg.长度为 L=1.2m的木板静止在光滑水平面上.其左端的壁上有自由长度为L0=0.6m的轻弹簧.右端放置一质量为m=1kg的小物块.小物块与木块间的动摩擦因数为μ=0.4.今对小物块施加一个水平向左的瞬时冲量I0=4N·s.小物块相对于木板向左运动而压缩弹簧使弹性势能增大为最大值Emax.接着小物块又相对于木板向右运动.最终恰好相对静止于木板的最右端.设弹簧未超出弹性限度.并取重力加速度为g=10m/s2.求: (1)当弹簧弹性势能最大时小物块速度v, (2)弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax. 解析:(1)由动量定理及动量守恒定律得 I0=mv0 mv0=(m+M)v 解得:v=1m/s (2)由动量守恒定律和功能关系得 mv0=(m+M)u mv2 =(m+M)v2+μmgLmax+Emax mv2 =(m+M)u2+2μmgLmax 解得:Emax=3J Lmax=0.75m
网址：http://m.1010jiajiao.com/timu3_id_1381680[举报]
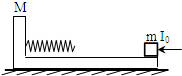如图所示，质量为M=3kg、长度为 L=1.2m的木板静止在光滑水平面上，其左端的壁上有自由长度为L0=0.6m的轻弹簧，右端放置一质量为m=1kg的小物块，小物块与木块间的动摩擦因数为μ=0.4，今对小物块施加一个水平向左的瞬时冲量I0=4N?s，小物块相对于木板向左运动而压缩弹簧使弹性势能增大为最大值Emax，接着小物块又相对于木板向右运动，最终恰好相对静止于木板的最右端，设弹簧未超出弹性限度，并取重力加速度为g=10m/s2．求：（1）当弹簧弹性势能最大时小物块速度v；
（2）弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax．
如图所示，质量为M=3kg、长度为 L=1.2m的木板静止在光滑水平面上，其左端的壁上有自由长度为L=0.6m的轻弹簧，右端放置一质量为m=1kg的小物块，小物块与木块间的动摩擦因数为μ=0.4，今对小物块施加一个水平向左的瞬时冲量I=4N?s，小物块相对于木板向左运动而压缩弹簧使弹性势能增大为最大值Emax，接着小物块又相对于木板向右运动，最终恰好相对静止于木板的最右端，设弹簧未超出弹性限度，并取重力加速度为g=10m/s2．求：
（1）当弹簧弹性势能最大时小物块速度v；
（2）弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax．
查看习题详情和答案>>
（1）当弹簧弹性势能最大时小物块速度v；
（2）弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax．
查看习题详情和答案>>
如图所示，质量为M=3kg、长度为L=1.2m的木板静止在光滑水平面上，其左端的壁上有自由长度为L0=0.6m的轻弹簧，右端放置一质量为m=1kg的小物块，小物块与木块间的动摩擦因数为μ=0.4，今对小物块施加一个水平向左的瞬时冲量I0=4N?s，小物块相对于木板向左运动而压缩弹簧使弹性势能增大为最大值Emax，接着小物块又相对于木板向右运动，最终恰好相对静止于木板的最右端，设弹簧未超出弹性限度，并取重力加速度为g=10m/s2．求：
（1）当弹簧弹性势能最大时小物块速度v；
（2）弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax．
查看习题详情和答案>>
（1）当弹簧弹性势能最大时小物块速度v；
（2）弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax．
如图所示，长L=1.6m，质量M=3kg的木板静放在光滑水平面上，质量m=1kg、带电量q=+2.5×10-4C的小滑块放在木板的右端，木板和物块间的动摩擦因数μ=0.1，所在空间加有一个方向竖直向下强度为E=4.0×104N/C的匀强电场，如图所示，现对木板施加一水平向右的拉力F．取g=10m/s2，求：（1）使物块不掉下去的最大拉力F；
（2）如果拉力F=11N恒定不变，小物块所能获得的最大动能．
如图所示，在竖直虚线MN的右侧存在着电场强度为E1=3×102N/C、方向竖直向上的匀强电场E1，在MN的左侧存在着水平方向的匀强电场E2．在右侧的匀强电场E1中，一条长为L=0.8m的绝缘细线一端固定在O点，另一端拴着质量m=0.3kg、电荷量q=2×10-2C的小球，O点到虚线MN的距离为x=1.2m．现将细线拉直到水平位置，使小球由静止释放，则小球能运动到图中的位置P（P点在O点的正上方）．（不计阻力，取g=10m/s2）（1）判断小球的电性；（不需要说明理由）
（2）求小球运动到P点的速度大小vp；
（3）若小球运动到P点时细线刚好断裂，细线断裂后小球继续运动，求小球运动到虚线MN处时速度大小；
（4）在（3）的情况下，若小球运动经过虚线MN后进入左侧的匀强电场E2恰能做直线运动，求匀强电场E2的大小．