摘要：在如图甲所示的直角坐标系中.原点O处固定有正点电荷Q.另有平行于y轴的匀强磁场.一个质量为m.带电荷量为+q的微粒.恰能以y轴上O′(0.a)点为圆心做匀速圆周运动.其轨迹平面与xOz平面平行.角速度为ω.旋转方向如图中箭头所示.试求匀强磁场的磁感应强度的大小和方向. 解析:微粒的受力情况如图乙所示. 由左手定则知磁感应强度的方向为y轴负方向.设粒子做圆周运动的轨迹半径为R.有: 库仑力F＝k 且cos θ＝ F洛＝BωRq 由题意可得:kcos θ＝mg 甲 乙 BωRq-k·sin θ＝mω2R 即BωRq-mg·＝mω2R 解得:B＝+. 答案:+.方向沿y轴负方向
网址：http://m.1010jiajiao.com/timu3_id_1377066[举报]
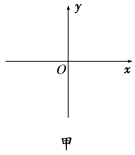
在如图甲所示的平面直角坐标系xOy中，存在沿x方向按如图乙所示规律周期性变化的匀强电场，沿x轴正方向为正。沿垂直于xOy平面指向纸里的方向存在按如图丙所示规律周期性变化的匀强磁场。在图甲中坐标原点O处有带正电的粒子，从t＝0时刻无初速度释放。已知粒子的质量m＝5×10－10kg，电荷量q＝1×10－6C，不计粒子的重力。求：
（1）t＝0.25×10－3s时粒子的速度及位置；
（2）t＝1×10－3s时粒子的位置坐标；
（3）t＝8×10－3s时粒子的速度。
（1）t＝0.25×10－3s时粒子的速度及位置；
（2）t＝1×10－3s时粒子的位置坐标；
（3）t＝8×10－3s时粒子的速度。
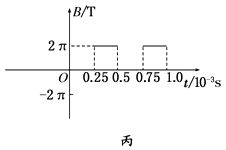
如图甲所示的平面直角坐标系xOy中，整个区域内存在匀强磁场，磁感应强度B随时间t的变化关系如图乙所示，(垂直纸面向里为正)，t＝0时刻，有一个带正电的粒子(不计重力)从坐标原点0沿x轴正方向进入磁场，初速度为v1＝2.0×103 m/s，已知带电粒子的比荷为1.0×104C/kg，试求：
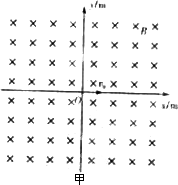
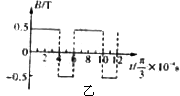
(1)
时刻，粒子的位置坐标；
(2)粒子从开始时刻起经过多长时间到达y轴；
(3)粒子返回原点所经历的时间．
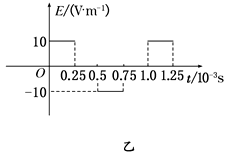
如图甲所示，M、N为水平放置的平行板电容器的两个极板，两极板间距d=0.1m，两极板间的电压U=12.5V，O为上极板中心的小孔，以O为坐标原点，在竖直平面内建立直角坐标系，在y轴方向上，0≤y≤2m区间存在方向与x轴平行的匀强电场（PQ为电场区域的上边界），在x轴方向上，电场范围足够大．若规定x轴正方向为电场正方向，电场强度随时间变化情况如图乙所示．现有一个带负电的粒子，在t=0时刻从紧靠M级板中心O'处无初速释放，经过小孔O进入N板上方的交变电场中，粒子的比荷q/m=1×102C/kg，不计粒子重力．求：
（1）粒子进入交变电场时的速度．
（2）粒子在两板之间飞行的时间．
（3）粒子在8×10-3s末的位置坐标．
（4）粒子离开交变电场时的速度大小和方向．
查看习题详情和答案>>
（1）粒子进入交变电场时的速度．
（2）粒子在两板之间飞行的时间．
（3）粒子在8×10-3s末的位置坐标．
（4）粒子离开交变电场时的速度大小和方向．
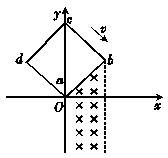
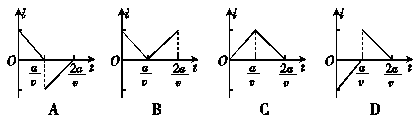
如图甲所示，在坐标系xOy中，有边长为L的正方形金属线框abcd，其对角线ac和y轴重合，顶点a位于坐标原点O处．在y轴右侧的第I象限内有一等腰直角三角形区域，直角边边长为L，底边的左端位于坐标原点O处，内有垂直纸面向里的匀强磁场．t=0时刻，线圈从图示位置沿cb方向，匀速穿过磁场区域．取a→b→c→d→a为感应电流的正方向，则在线圈穿越磁场区域的过程中，感应电流i、ab间的电势差Uab．随时间t变化的图线应是乙图中的（ ）
