摘要：如图所示.一半径为R的光滑绝缘半球面开口向下.固定在水平面上.整个空间存在匀强磁场.磁感应强度方向竖直向下.一电荷量为q(q>0).质量为m的小球P在球面上做水平的匀速圆周运动.圆心为O′.球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ<).为了使小球能够在该圆周上运动.求磁感应强度大小的最小值及小球P相应的速率.(重力加速度为g)[2008年高考·四川理综卷] 解析:据题意.小球P在球面上做水平的匀速圆周运动.该圆周的圆心为 O′.P受到向下的重力mg.球面对它沿OP方向的支持力FN和磁场的洛伦兹力F＝qvB(式中v为小球运动的速率). 洛伦兹力F的方向指向 O′.根据牛顿第二定律有: FNcos θ-mg＝0 F-FNsin θ＝m 由以上各式可得: v2-v+＝0 由于v是实数.必须满足 Δ＝()2-≥0 由此得:B≥ 可见.为了使小球能够在该圆周上运动.磁感应强度大小的最小值为: Bmin＝ 此时.带电小球做匀速圆周运动的速率为: v＝ 即v＝sin θ. 答案: sin θ
网址：http://m.1010jiajiao.com/timu3_id_1377059[举报]
如图所示，一半径为R的绝缘圆形轨道竖直放置，圆轨道最低点与一条水平轨道相连，轨道都是光滑的．轨道所在空间存在水平向右的匀强电场，场强为E．从水平轨道上的A点由静止释放一质量为m的带正电的小球，为使小球刚好在圆轨道内做圆周运动，已知小球受到的电场力大小等于小球重力的| 3 | 4 |
（1）小球在圆周上的最小速度是多少？
（2）在B时小球对轨道的压力是多少？
（3）释放点A距圆轨道最低点B的距离s．
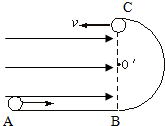如图所示，一半径为R的绝缘圆形轨道竖直放置，BC为圆轨道的直径，圆轨道最低点与一条水平轨道相连．已知所有的轨道均为光滑的，水平轨道所在空间存在水平向右的匀强电场．从水平轨道上的A点由静止释放一质量为m，电量为q的带正电的小球，已知小球恰好能从A点运动2.5R的距离到达B点进入圆轨道，并恰能通过圆轨道的顶端C点．求：（1）小球在C点的速度大小；
（2）电场强度E；
（3）小球最终的落地点离B点距离是多少？
（4）小球落地时的末速度是多少？
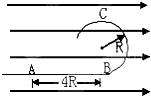如图所示，一半径为R的绝缘圆形轨道竖直放置，圆轨道最低点与一条水平轨道相连，轨道都是光滑的，轨道所在空间存在水平向右的匀强电场，从水平轨道上的A点由静止释放一质量为m带正电的小球，释放点A距圆轨道最低点B的距离为4R，已知电场力大小等于小球重力的| 3 | 4 |
（1）小球的速度为多大？
（2）轨道对小球的弹力多大？
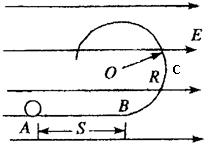如图所示，一半径为R的绝缘圆形轨道竖直放置，圆轨道最低点B点与一条水平轨道相连，轨道都是光滑的，轨道所在空间存在水平向右、场强为E的匀强电场，从水平轨道上的A点由静止释放一质量为m带正电的小球，设A、B间的距离为S．已知小球受到的电场力大小等于小球重力的3/4倍，C点为圆形轨道上与圆心O的等高点．（重力加速度为g）
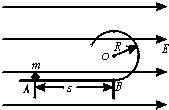如图所示，一半径为R的绝缘圆形轨道竖直放置，圆轨道最低点与一条水平轨道相连，轨道都是光滑的．轨道所在空间存在水平向右的匀强电场，场强为E．从水平轨道上的A点由静止释放一质量为m的带正电的小球，为使小球刚好在圆轨道内做圆周运动，求释放点A距圆轨道最低点B的距离s．已知小球受到的电场力大小等于小球重力的