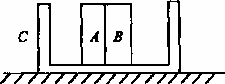
摘要:光滑水平面上放着质量mA=1 kg的物块A与质量mB=2 kg的物块B.A与B均可视为质点.A靠在竖直墙壁上.A.B间夹一个被压缩的轻弹簧(弹簧与A.B均不拴接).用手挡住B不动.此时弹簧弹性势能Ep=49 J.在A.B间系一轻质细绳.细绳长度大于弹簧的自然长度.如图所示.放手后B向右运动.绳在短暂时间内被拉断.之后B冲上与水平面相切的竖直半圆光滑轨道.其半径R=0.5 m.B恰能到达最高点C.取g=10 m/s2.求: (1)绳拉断后瞬间B的速度vB的大小, (2)绳拉断过程绳对B的冲量I的大小, (3)绳拉断过程绳对A所做的功W.[2008年高考·天津理综卷] 分析:A.B系统的运动可以分为以下过程: (1)弹簧推B物体至绳子伸直前, (2)绳子伸直至被拉断, (3)B运行至最高点过程. 分析清物体的运动过程.问题就变得很清晰了. 解析:(1)设B在绳被拉断后瞬间的速度为vB.到达C点时的速度为vC.有: mBg=mB mBv=mBv+2mBgR 代入数据得:vB=5 m/s. (2)设弹簧恢复到自然长度时B的速度为v1.取水平向右为正方向.有: Ep=mBv I=mBvB-mBv1 代入数据得:I=-4 N·s.其大小为4 N·s. (3)设绳断后A的速度为vA.取水平向右为正方向.有: mBv1=mBvB+mAvA W=mAv 代入数据得:W=8 J. 答案:4 N·s (3)8 J
网址:http://m.1010jiajiao.com/timu3_id_1376747[举报]
光滑水平面上放着质量mA =1 kg的物块A与质量为mB =2 kg的物块B,A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能为Ep=49 J.在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示.放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5 m,B恰能运动到最高点C.取g=10 m/s2,求

(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I的大小;
(3)绳拉断过程绳对A所做的功W.
光滑水平面上放着质量
mA=1 kg的物块A与质量mB=2 kg的物块B,A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能EP=49 J.在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示.放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5 m,B恰能到达最高点C.取g=10 m/s2,求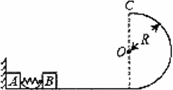
(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I的大小;
(3)绳拉断过程绳对A所做的功W.
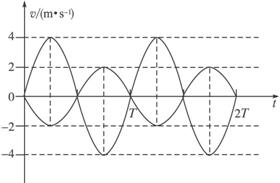
如图,光滑水平面上固定着一对竖直放置的平行金属板G和H。在金属板G右壁固定一个可视为质点的小球C,其质量为 Mc=0.01 kg 、带电荷量为q=+1×10-5 C 。G、H两板间距离为d=10 cm ,板H下方开有能让小球C自由通过的小洞。质量分别为Ma=0.01 kg 和Mb=0.02 kg 的不带电绝缘小球A、B用一轻质弹簧连接,并用细线拴连使弹簧处于压缩状态,静放在H板右侧的光滑水平面上,如图a所示。现将细线烧断,小球A、B在弹簧作用下做来回往复运动(A球不会进入G、H两板间)。以向右为速度的正方向,从细线断开后的某时刻开始计时,得到A球的速度—时间图象如图(b)所示。
图(a)

图(b)
(1)求在t=0、![]() 、
、![]() 时刻小球B的速度,并在图(b)中大致画出B球的速度—时间图象;
时刻小球B的速度,并在图(b)中大致画出B球的速度—时间图象;
(2)若G、H板间是电场强度为E=8×104 V/m的匀强电场,在某时刻将小球C释放,则小球C离开电场时的速度为多大?若小球C以离开电场时的速度向右匀速运动,它将遇到小球A,并与之结合在一起运动,试定量分析在各种可能的情况下弹簧的最大弹性势能(即最大弹性势能的范围)。
查看习题详情和答案>>