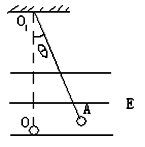
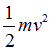摘要：绝缘细绳的一端固定在天花板上.另一端连接着一个带负电的电荷量为q.质量为m的小球.当空间存在水平方向的匀强电场后.绳稳定处于与竖直方向成θ＝60°角的位置．如图6-2-15所示.已知细绳长为L.让小球从θ＝30°的A点释放.则( ) 图6-2-15 A．匀强电场的场强为 B．匀强电场的场强为 C．小球的最大速度为 D．小球的最大速度为(-1) 解析:小球在θ＝60°时处于平衡.则Eq＝mgtan θ.所以E＝＝.选项A错误.B正确,小球第一次到达平衡位置处的速度是小球的最大速度.根据动能定理有:qE(Lsin 60°-Lsin 30°)-mg(Lcos 30°-Lcos 60°)＝mv2. 联立解得v＝(-1).选项C错误.D正确． 答案:BD
网址：http://m.1010jiajiao.com/timu3_id_1374657[举报]
绝缘细绳的一端固定在天花板上，另一端连接着一个带负电的电量为q、质量为m的小球，当空间建立水平方向的匀强电场后，绳稳定处于与竖直方向成θ=600角的位置，如图所示．（1）求匀强电场的场强E；
（2）若细绳长为L，让小球从θ=30°的A点释放，王明同学求解小球运动至某点的速度的过程如下：
据动能定理-mgL（1-cos30°）+qELsin30°=
| 1 |
| 2 |
2(
|
（8分）绝缘细绳的一端固定在天花板上，另一端连接着一个带负电的电量为q、质量为m的小球，当空间中有水平方向的匀强电场后，长为L的绳稳定在与竖直方向成θ=300角的A位置，如图所示。求：
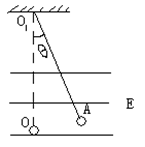
（1）匀强电场的场强E；
（2）将小球从O点由静止释放，则到A处时电场力做的功为多少？
（3）小球由静止从O点运动到A点过程中，电势能减少了多少？
查看习题详情和答案>>绝缘细绳的一端固定在天花板上，另一端连接着一个带电量为q、质量为m的小球，当空间建立水平方向的匀强电场后，绳稳定处于与竖直方向成
角的位置，如图17所示。求：若细绳长为L，让小球从
角处释放，王明同学求解小球运动至某点的速度的过程如下：由动能定理 
得： 
你认为王明同学求的是小球到达最低点O'的速度，还是到达
角即平衡位置处的速度？如果都不正确的话，解出正确结果。
