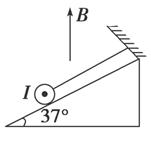
摘要:12. 图4-2-26 如图4-2-26所示.小球从光滑的圆弧轨道下滑至水平轨道末端时.光电装置被触动.控制电路会使转筒立刻以某一角速度匀速连续转动起来.转筒的底面半径为R.已知轨道末端与转筒上部相平.与转筒的转轴距离为L.且与转筒侧壁上的小孔的高度差为h,开始时转筒静止.且小孔正对着轨道方向.现让一小球从圆弧轨道上的某处无初速滑下.若正好能钻入转筒的小孔(小孔比小球略大.小球视为质点.不计空气阻力.重力加速度为g).求: (1)小球从圆弧轨道上释放时的高度为H, (2)转筒转动的角速度ω. 解析:(1)设小球离开轨道进入小孔的时间为t.则由平抛运动规律得h=gt2. L-R=v0t 小球在轨道上运动过程中机械能守恒.故有mgH=mv 联立解得:t= .H=. (2)在小球做平抛运动的时间内.圆筒必须恰好转整数转.小球才能钻进小孔. 即ωt=2nπ(n=1,2,3-).所以ω=nπ (n=1,2,3-) 答案:nπ (n=1,2,3-) () 来源: 版权所有:() 版权所有:() 版权所有:()
网址:http://m.1010jiajiao.com/timu3_id_1374611[举报]
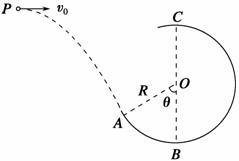
如图5-2-26所示,一个质量为0.6 kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3 m,θ=60°,小球到达A点时的速度vA=4 m/s.(取g=10 m/s2)求:
(1)小球做平抛运动的初速度v0;
(2)P点与A点的水平距离和竖直高度;
(3)小球到达圆弧最高点C时对轨道的压力.
![]()
如图9-2-26甲所示,空间存在一宽度为2L的有界匀强磁场,磁场方向垂直纸面向里.在光滑绝缘水平面内有一边长为L的正方形金属线框,其质量m=1 kg、电阻R=4 Ω,在水平向左的外力F作用下,以初速度v0=4 m/s匀减速进入磁场,线框平面与磁场垂直,外力F大小随时间t变化的图线如图乙所示.以线框右边刚进入磁场时开始计时.
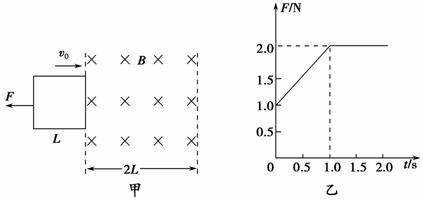
图9-2-26
(1)求匀强磁场的磁感应强度B;
(2)求线框进入磁场的过程中,通过线框的电荷量q;
(3)判断线框能否从右侧离开磁场?说明理由.
查看习题详情和答案>>如图1-2-25所示, 波源P从平衡位置y=0开始振动,方向竖直向上(y轴的正方向),振动周期T=0.01 s.产生的简谐波向右传播,波速为v=80 m/s.经过一段时间后,S、Q两点开始振动,已知距离SP=0.4 m、SQ=1.0 m.若以Q点开始振动的时刻作为计时的零点,则下列说法正确的是 ( ).
A.图1-2-26乙能正确描述Q点的振动情况
B.图1-2-26甲能正确描述S点的振动情况
C.图1-2-26丙能正确描述t=0时刻的波形图
D.若在Q点也存在一个波源,振动情况同波源P,则S为振动加强点
![]()
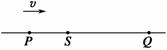

图1-2-26
查看习题详情和答案>>