摘要：如图甲所示.斜面体b的质量为M.放在粗糙的水平地面上.质量为m的滑块a以一定的初速度沿粗糙的斜面向上滑.然后又返回.此过程中b没有相对地面移动.由此可知( ) A.地面对b一直有向右的摩擦力 B.地面对b一直有向左的摩擦力 C.地面对b的摩擦力方向先向左后向右 D.地面对b的支持力一直小于(M+m)g 解析:在a向上滑的过程中.a.b的受力情况分别如图乙.丙所示.则有: f2＝FN1′sin θ+f1′cos θ＝mgcos θsin θ+μmgcos2 θ.方向向左 FN2＝Mg+FN1′cos θ-f1′sin θ ＝Mg+mgcos2 θ-μmgcos θsin θ<(M+m)g. 当a下滑时.由mgsin θ>μmgcos θ可得摩擦力的水平分力小于正压力的水平分力.故知斜面体有向右滑行的趋势.地面对它的静摩擦力向左. 答案:BD
网址：http://m.1010jiajiao.com/timu3_id_1373982[举报]
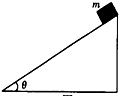如图甲所示，斜面体固定在水平面上，倾角为θ=30°，质量为m的物块从斜面体上由静止释放，以加速度a=| g |
| 2 |
A、 |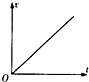
B、 |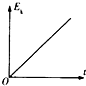
C、 |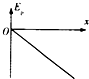
D、 |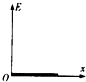
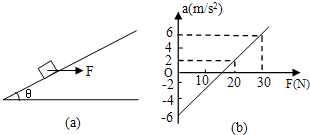如图甲所示，用一水平外力F推着一个静止在倾角为θ的光滑斜面上的物体，逐渐增大F，物体做变加速运动，其加速度a随外力F变化的图象如图乙所示，若重力加速度g取10m/s2．根据图乙中所提供的信息不能计算出（ ）
查看习题详情和答案>>
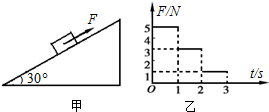如图甲所示，倾角为30°的足够长的光滑斜面上，有一质量m=0.8kg的物体受到平行斜面向上的力F作用，其大小F随时间t变化的规律如图乙所示，t=0时刻物体速度为零，重力加速度g=10m/s2．下列说法中正确的是（ ）
查看习题详情和答案>>
如图甲所示，在倾角为θ的光滑斜面上，有一个质量为m的物体在沿斜面方向的力F的作用下由静止开始运动，物体的机械能E随位移x的变化关系如图乙所示．其中0～x1过程的图线是曲线，x1～x2过程的图线为平行于x轴的直线，则下列说法中正确的是（ ）
查看习题详情和答案>>
如图甲所示，一个绝缘倾斜直轨道固定在竖直面内，轨道的AB部分粗糙，BF部分光滑．整个空间存在着竖直方向的周期性变化的匀强电场，电场强度随时间的变化规律如图乙所示，t=0时电场方向竖直向下．在虚线的右侧存在着垂直纸面向里的匀强磁场，磁感应强度为B=
．现有一个质量为m，电量为q的带正电的物体（可以视为质点），在t=0时从A点静止释放，物体与轨道间的动摩擦因数为μ，t=2s时刻，物体滑动到B点．在B点以后的运动过程中，物体没有离开磁场区域，物体在轨道上BC段的运动时间为1s，在轨道上CD段的运动时间也为1s．（物体所受到的洛伦兹力小于2mgcosθ）
（1）若轨道倾角为θ，求物块滑动到B的速度大小．
（2）若轨道倾角θ角未知，而已知BC及CD的长度分别为S1、S2，求出倾角θ的三角函表达式（用S1、S2、g表示）
（3）观察物体在D点以后的运动过程中，发现它并未沿着斜面运动，而且物块刚好水平打在H点处的竖直挡板（高度可以忽略）上停下，斜面倾角θ已知，求F点与H点的间距L．
查看习题详情和答案>>
| 2πm | q |
（1）若轨道倾角为θ，求物块滑动到B的速度大小．
（2）若轨道倾角θ角未知，而已知BC及CD的长度分别为S1、S2，求出倾角θ的三角函表达式（用S1、S2、g表示）
（3）观察物体在D点以后的运动过程中，发现它并未沿着斜面运动，而且物块刚好水平打在H点处的竖直挡板（高度可以忽略）上停下，斜面倾角θ已知，求F点与H点的间距L．