网址：http://m.1010jiajiao.com/timu3_id_1363544[举报]
为了测定气垫导轨上滑块的加速度，滑块上安装了宽度为3.0 cm的遮光板，如图1－1－4所示，滑块在牵引力作用下先后匀加速通过两个光电门，配套的数字毫秒计记录了遮光板通过第一个光电门的时间为Δt1＝0.30 s，通过第二个光电门的时间为Δt2＝0.10 s，遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为Δt＝3.0 s。试估算：
图1－1－4
(1)滑块的加速度多大？
(2)两个光电门之间的距离是多少？
解析：(1)遮光板通过第一个光电门的速度
v1＝
＝
m/s＝0.10 m/s
遮光板通过第二个光电门的速度
v2＝
＝
m/s＝0.30 m/s
故滑块的加速度a＝
≈0.067 m/s2。
(2)两个光电门之间的距离x＝
Δt＝0.6 m。
答案：(1)0.067 m/s2 (2)0.6 m
查看习题详情和答案>>解析 (1)整个装置沿斜面向上做匀速运动时，即整个系统处于平衡状态，
则研究A物体：f＝mAgsin θ＝2 N，
研究整体：F＝(mA＋mB)gsin θ＋μ2(mA＋mB)gcos θ＝21 N.
(2)整个装置沿斜面向上做匀加速运动，且A、B恰好没有相对滑动，则说明此时A、B之间恰好达到最大静摩擦力，
研究A物体：
fmax＝f滑＝μ1mAgcos θ＝2.4 N，
fmax－mAgsin θ＝mAa，
解得a＝1 m/s2，
研究整体：F－(mA＋mB)gsin θ－μ2(mA＋mB)gcos θ＝(mA＋mB)a，
解得F＝23.4 N.
答案 (1)2 N 21 N (2)2.4 N 23.4 N
查看习题详情和答案>>解析 (1)设木板第一次上升过程中，物块的加速度为a物块，由牛顿第二定律kmgsin θ－mgsin θ＝ma物块
解得a物块＝(k－1)gsin θ，方向沿斜面向上
(2)设以地面为零势能面，木板第一次与挡板碰撞时的速度大小为v1
由机械能守恒得：
×2mv
＝2mgH
解得v1＝
设木板弹起后的加速度为a板，由牛顿第二定律得：
a板＝－(k＋1)gsin θ
木板第一次弹起的最大路程s1＝
＝
木板运动的路程s＝
＋2s1＝
(3)设物块相对木板滑动距离为L
根据能量守恒mgH＋mg(H＋Lsin θ)＝kmgLsin θ
摩擦力对木板及物块做的总功W＝－kmgLsin θ
解得W＝－
答案 (1)(k－1)gsin θ；方向沿斜面向上
(2) (3)－
解析 (1)小球从曲面上滑下，只有重力做功，由机械能守恒定律知：
mgh＝mv
①
得v0＝
＝
m/s＝2 m/s.
(2)小球离开平台后做平抛运动，小球正好落在木板的末端，则
H＝gt2 ②
＝v1t ③
联立②③两式得：v1＝4 m/s
设释放小球的高度为h1，则由mgh1＝mv
得h1＝
＝0.8 m.
(3)由机械能守恒定律可得：mgh＝mv2
小球由离开平台后做平抛运动，可看做水平方向的匀速直线运动和竖直方向的自由落体运动，则：
y＝gt2 ④
x＝vt ⑤
tan 37°＝
⑥
vy＝gt ⑦
v
＝v2＋v
⑧
Ek＝mv ⑨
由④⑤⑥⑦⑧⑨式得：Ek＝32.5h ⑩
考虑到当h>0.8 m时小球不会落到斜面上，其图象如图所示
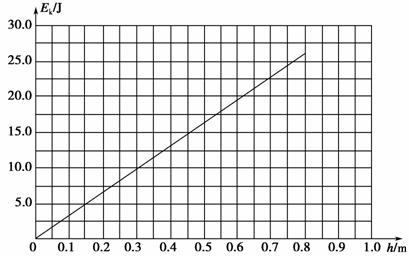
答案 (1)2 m/s (2)0.8 m (3)Ek＝32.5h 图象见解析
查看习题详情和答案>>
；(或因为sin θ1＝
，sin θ2＝
，
＝
)．