如图所示，abcd为质量m′=4kg的U形导轨，放在光滑绝缘的水平面上，其ab边与cd边平行且与bc边垂直，ad端为开口端．另有一根质量m=1.2kg的金属棒PQ平行bc放在水平导轨上，PQ左边用固定的竖直绝缘立柱e、f挡住PQ使其无法向左运动，处于匀强磁场中，磁场以OO′为界，左侧的磁场方向竖直向上，右侧的磁场方向水平向右，磁感应强度大小均为B=1.6T．导轨的bc段长l=0.5m，其电阻r=0.8Ω，金属棒PQ的电阻R=0.4Ω，其余电阻均可不计，金属棒PQ与导轨间的动摩擦因数μ=0.2．若在导轨上作用一个方向向左、大小为F=4N的水平拉力，设导轨足够长，g取10m/s²，求：
（1）导轨运动的最大加速度；
（2）流过导轨的最大电流；
（3）拉力F的最大功率．

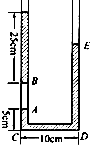如图所示，截面均匀的U形玻璃细管两端都开口，玻璃管足够长，管内有两段水银柱封闭着一段空气柱．若气体温度是27℃时，空气柱在U形管的左侧．A、B两点之间封闭着的空气柱长为15cm，U形管底长CD=10cm，AC高为5cm．已知此时的大气压强为75cmHg．
（1）若保持气体的温度不变，从U形管左侧管口处缓慢地再注入25cm长的水银柱，则管内空气柱长度为多少？
（2）为了使这段空气柱长度恢复到15cm，且回到A、B两点之间．可以向U形管再注入一些水银，且可改变气体的温度，应从哪一侧管口注人多长水银柱？气体的温度变为多少？

如图所示，左侧为一个半径为R的半球形的碗固定在水平桌面上，碗口水平，O点为球心，碗的内表面及碗口光滑．右侧是一个固定光滑斜面，斜面足够长，倾角θ=30°．一根不可伸长的不计质量的细绳跨在碗口及光滑斜面顶端的光滑定滑轮两端上，线的两端分别系有可视为质点的小球m₁和m₂，且m₁＞m₂．开始时m₁恰在右端碗口水平直径A处，m₂在斜面上且距离斜面顶端足够远，此时连接两球的细绳与斜面平行且恰好伸直．当m₁由静止释放运动到圆心O的正下方B点时细绳突然断开，不计细绳断开瞬间的能量损失．

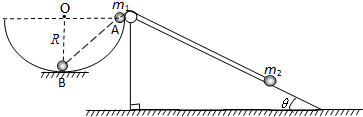
（1）求小球m₂沿斜面上升的最大距离s；
（2）若已知细绳断开后小球m₁沿碗的内侧上升的最大高度为R/2，求

m1

m2

=．

如图所示，截面均匀的U形玻璃细管两端都开口，玻璃管足够长，管内有两段水银柱封闭着一段空气柱，若气柱温度是27℃时，空气柱在U形管的左侧，A、B两点之间封闭着的空气柱长为15cm，U形管底边长CD=10cm，AC高为5cm．已知此时的大气压强为75cmHg．
（1）若保持气体的温度不变，从U形管左侧管口处缓慢地再注入25cm长的水银柱，则管内空气柱长度为多少？
某同学是这样解的：对AB部分气体，初态p₁=100cmHg，V₁=15Scm³，末态p₂=125cmHg，V₂=LScm³，则由玻意耳定律p₁V₁=p₂V₂解得管内空气柱长度L=12cm．以上解法是否正确，请作出判断并说明理由，如不正确则还须求出此时管内空气柱的实际长度为多少？
（2）为了使这段空气柱长度恢复到15cm，且回到A、B两点之间，可以向U形管中再注入一些水银，且改变气体的温度．问：应从哪一侧管口注入多长的水银柱？气体的温度变为多少？