摘要：24．如图8所示.在真空中.半径 的圆形区域内存在垂直纸面向外的匀强磁场.磁 感应强度大小为B.在此区域外围空间有垂直纸 而向内的大小也为B的磁场.一个带电粒子从边 界上的P点沿半径向外.以速度进入外围磁场. 已知带电粒子质量.带电量 .不计重力.磁感应强度. 粒子运动速度.求:粒子第一次 回到P点所需时间.并画出粒子运动轨迹图.
网址：http://m.1010jiajiao.com/timu3_id_1229965[举报]
如图8所示，带电粒子在真空环境中的匀强磁场里按图示径迹运动.径迹为互相衔接的两段半径不等的半圆弧，中间是一块薄金属片，粒子穿过时有动能损失.试判断粒子在上、下两段半圆径迹中哪段所需时间较长？（粒子重力不计）
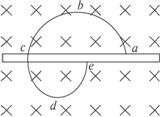
图8
查看习题详情和答案>>（18分）如图8所示，真空中有一以（r，0）为圆心、半径为r的圆柱形匀强磁场区域，磁场的磁感应强度大小为B、方向垂直纸面向里，在y≥r的范围内，有方向向左的匀强电场，电场强度大小E。从O点向不同方向发射速率相同的质子，质子的运动轨迹均在纸面内，已知质子的电量为e，质量为m，质子在磁场中的偏转半径也为r，不计重力及阻力作用。求：
（1）质子进入磁场时的速度大小；
（2）速度方向沿x轴正方向射入磁场的质子，到达y轴所需的时间；
（3）速度方向与x轴正方向成30o角（如图中所示）射入磁场的质子，到达y轴时的位置
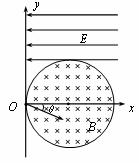
查看习题详情和答案>>
如图所示，斜面轨道AB与水平面之间的夹角θ=53°，BD为半径R=4m的圆弧形轨道，且B点与D点在同一水平面上，在B点，轨道AB与圆弧形轨道BD相切，整个轨道处于竖直平面内且处处光滑，在A点处的一质量m=1kg的小球由静止滑下，经过B、C点后从D点斜抛出去，最后落在地面上的S点处时的速度大小vs=8m/s，已知A点距地面的高度H=10m，B点距地面的高度h=5m，设以MDN为分界线，其左边为一阻力场区域，右边为真空区域，g取10m/s2，sin53°=0.8，cos53°=0.6（1）小球经过B点的速度为多大？
（2）小球经过圆弧轨道最低处C点时对轨道的压力多大？
（3）小球从D点抛出后，受到的阻力f与其瞬时速度方向始终相反，求小球从D点至S点的过程中，阻力f所做的功．
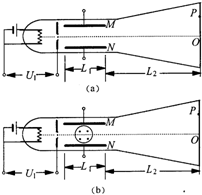如图（a）所示的真空管中，电子从灯丝K发出 （初速不计），经电压为U1的加速电场加速后沿中心线进入两平行金属板M，N间的匀强电场中，通过电场后打到荧光屏上的P点处，设M，N板间电压为U2，两板距离为d，板长为Ll，板右端到荧光屏的距离为L2，已知U1=576V，U2=168V，L1=6cm，d=3cm，L2=21cm，电子的比荷| e | m |
（1）电子离开偏转电场时的偏角θ（即电子离开偏转电场时速度与进入偏转电场时速度的夹角）．
（2）电子打到荧光屏上的位置户偏离荧光屏中心O的距离OP．
（3）若撤去M、N间的电压U2，而在两平行板中的圆形区域内（如图b所示）加一磁感应强度为B=0.001T的匀强磁场，圆形区域的中心正好就是两平行板空间部分的中心．要使电子通过磁场后仍打在荧光屏上的P点处，圆形区域的半径r为多少？（结果中可含有反三角函数）