题目内容
如图8所示，带电粒子在真空环境中的匀强磁场里按图示径迹运动.径迹为互相衔接的两段半径不等的半圆弧，中间是一块薄金属片，粒子穿过时有动能损失.试判断粒子在上、下两段半圆径迹中哪段所需时间较长？（粒子重力不计）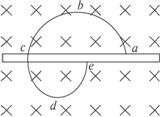
图8
解析：首先根据洛伦兹力方向（指向圆心），磁场方向以及动能损耗情况，判定粒子带正电，沿abcde方向运动.
再求通过上、下两段圆弧所需时间：带电粒子在磁场中做匀速圆周运动f洛=f向
Bqv0=ma向=mωv0=mv0
回旋周期T=
,T仅由磁感应强度B及粒子的比荷决定，与粒子速度v、回旋半径R无关.因此上、下两半圆弧粒子通过所需时间相等.动能的损耗导致粒子的速度减小，结果使得回旋半径按比例减小，周期并不改变.
答案：所需时间相等
练习册系列答案
相关题目
回旋加速器是获得高能带电粒子的装置，其核心部分是分别与高频交流电源的两极相连接的两个D形金属盒，两盒间的狭缝中形成周期性变化的电场，使粒子在通过狭缝时都能得到加速，两D形金属盒处于垂直于盒底的匀强磁场中，如图8所示．若要增大带电粒子从D形盒中射出时的动能，可采用的方法是（ ）
| A．增大磁场的磁感应强度 |
| B．增大电场的加速电压 |
| C．增大狭缝的距离 |
| D．增大D形金属盒的半径 |
