北京东城区
2008―2009学年度高三第二学期统一练习(二)
数学试题(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.不能答在试卷上.
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知集合 的集合N的个数是 ( )
的集合N的个数是 ( )
A.1 B.2 C.3 D.4
2. 处连续的 ( )
处连续的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3. 在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本
①采用随机抽样法:抽签取出20个样本;
②采用系统抽样法:将零件编号为00,01……,99,然后平均分组抽取20个样本;
③采用分层抽样法:从一级品,二级品,三级品中抽取20个样本。
下列说法中正确的是 ( )
A.无论采用哪种方法,这100个零件中每一个被抽到的概率都相等
B.①②两种抽样方法,这100个零件中每一个被抽到的概率都相等;③并非如此
C.①②两种抽样方法,这100个零件中每一个被抽到的概率都相等;②并非如此
D.采用不同的抽样方法,这100个零件中每一个零件被抽到的概率是各不相同的
4.在 的系数分别为a,b,如果
的系数分别为a,b,如果 的值为 ( )
的值为 ( )
A.70 B.60 C.55 D.40
5.设数列 ,且对任意的
,且对任意的 ,则{
,则{ }的前n项和为Sn为 ( )
}的前n项和为Sn为 ( )
A. B.
B. C.
C. D.
D.
6.已知直线l1//平面 ,直线
,直线 ,点
,点 的距离为a,A到l2的距离为b,A,B两点间的距离为c,则 ( )
的距离为a,A到l2的距离为b,A,B两点间的距离为c,则 ( )
A. B.
B. C.
C. D.
D.
7.若 则角
则角 的终边落在直线( )上 ( )
的终边落在直线( )上 ( )
A. B.
B. C.
C. D.
D.
8.已知P为抛物线 上动点,F为抛物线的焦点,过F作抛物线在P点处的切线的垂线,垂足为G,则点G的轨迹方程为 ( )
上动点,F为抛物线的焦点,过F作抛物线在P点处的切线的垂线,垂足为G,则点G的轨迹方程为 ( )
A. B.
B.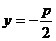
C. D.
D.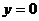
第Ⅱ卷(共110分)
注意事项:
1.用钢笔或圆珠笔将答案直接写在试卷上。
2.答卷前将密封线内的项目填写清楚。
二、填空题:本大题共6小题,每小题5分,共30分。把答案填在题中横线上。
9.设函数 的值为
.
的值为
.
10.已知过原点的直线与圆 (其中
(其中 为参数)相切,若切点在第二象限,则该直线的方程为
.
为参数)相切,若切点在第二象限,则该直线的方程为
.
|
 条弦,它们的长构成等比数列{
条弦,它们的长构成等比数列{ ,则n的值为
.
,则n的值为
. 且
且 。
。 ,求角A的值。
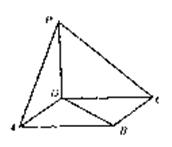
,求角A的值。 M、N分别为AB,SB的中点。
M、N分别为AB,SB的中点。
 m,通过铁丝BC、CA1、CA2、CA3(A1、A2、A3是圆上三等分点)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。
m,通过铁丝BC、CA1、CA2、CA3(A1、A2、A3是圆上三等分点)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。 ,铁丝总长为
,铁丝总长为 ,试写出y关于x的函数解析式,并写出函数定义域;
,试写出y关于x的函数解析式,并写出函数定义域;
 ,每次命中与否互相独立。
,每次命中与否互相独立。 ,求
,求 的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为菱形。
的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为菱形。
 (其中a为常数,
(其中a为常数, ),利用函数
),利用函数
 方法如下:
方法如下: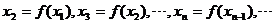
 的通项公式;
的通项公式; }?若存在,求出a的值;若不存在,请说明理由。
}?若存在,求出a的值;若不存在,请说明理由。 10.
10. 11.
11. 12.
12. 13.50 14.5
13.50 14.5 ………………2分
………………2分
 ……………………3分
……………………3分 ……………………5分
……………………5分 ,
, …………………………6分
…………………………6分
 …………………………7分
…………………………7分
 ,
, .
. .……………………11分
.……………………11分 ……………………12分
……………………12分
 ……………………13分
……………………13分 DE⊥CM,BM⊥CM,
DE⊥CM,BM⊥CM,

 ,
,

 .
. ……………………14分
……………………14分
 )
) ),
), ),
),




 为平面ABC的法向量,
为平面ABC的法向量,
 ……………………………………………14分
……………………………………………14分 ……………………………………4分
……………………………………4分 (0<x<2)……………………………5分
(0<x<2)……………………………5分 ……………………………………8分
……………………………………8分 =0得
=0得 解得
解得 或
或 (舍),……10分
(舍),……10分
 ……………………………………4分
……………………………………4分 的可能取值为2,3,4,5。…………………………………5分
的可能取值为2,3,4,5。…………………………………5分 =
= ;
; =
= ;
; =
= ;
; =
= 。……………………………………11分
。……………………………………11分 的分布列为
的分布列为






 …………………………………………………3分
…………………………………………………3分

 解得
解得 或
或 (舍)。
(舍)。
 ,又
,又 故
故 。
。 。
。 ,由
,由 得
得 即
即 a
a
 即
即 7分
7分 ,故直线AB的方程为
,故直线AB的方程为 8分
8分 10分
10分 得
得
 ,则
,则
 13分
13分 ,所以
,所以
 ,即
,即 =-1,又
=-1,又
 是首项为―1,公差d= ―1的等差数列………………3分
是首项为―1,公差d= ―1的等差数列………………3分 ,
,
 的通项公式为
的通项公式为 ……………………4分
……………………4分 时,方程
时,方程 有解,………………5分
有解,………………5分 有不等式a的解
有不等式a的解 ,得
,得 .
. ……………………10分
……………………10分 },
}, 中无解,……………………12分
中无解,……………………12分 无实数解.
无实数解. 的解。
的解。 无实数解,
无实数解, ,
,