2009年高考数学第二轮执点专题测试:不等式(含详解)
一、选择题:
1、下列不等式正确的是( )
(A)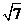 -
-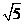 >
>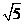 -
-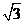 (B)
(B)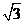 +
+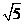 >
>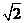 +
+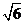
(C)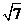 +
+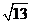 >3+
>3+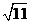 (D)5+
(D)5+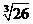 >8
>8
2、已知集合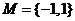 ,
,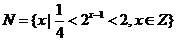 则
则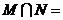 ( )
( )
(A) 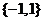 (B)
(B) 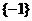 (C)
(C) 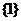 (D)
(D)
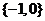
3、设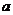 ,b是两个实数,且
,b是两个实数,且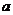 ≠b,
≠b,
①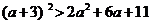 ;②
;②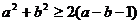 ;③
;③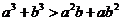 ;④
;④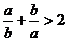 。
。
上述4个式子中恒成立的有 ( )
(A)1个 (B)2个 (C)3个 (D)4个
4、对于实数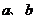 ,“
,“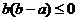 ”是“
”是“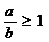 ”成立的( )
”成立的( )
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D) 既不充分又不必要条件
5、若关于x的不等式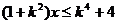 的解集是M,则对任意实数k,总有 ( )
的解集是M,则对任意实数k,总有 ( )
A.2∈M,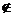 M B.2
M B.2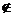 M,0
M,0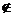 M C.2
M C.2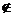 M,0∈M D.2∈M ,0∈M
M,0∈M D.2∈M ,0∈M
6、函数y=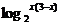 的定义域是( )
的定义域是( )
(A){xㄏ0<x<3} (B){xㄏx<0或x>3}
(C){xㄏx≤0或x≥3} (D){xㄏ0≤x≤3}
7、已知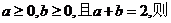 ( )
( )
(A)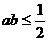 (B)
(B)
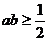 (C)
(C)
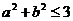 (D)
(D)
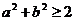
8、若不等式f(x)=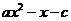 >0的解集
>0的解集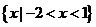 ,则函数y=f(-x)的图象为( )
,则函数y=f(-x)的图象为( )
9.若直线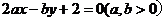 始终平分圆
始终平分圆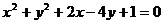 的周长,则
的周长,则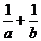 的最小值是( )
的最小值是( )
A.4 B.2 C.
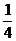 D.
D.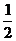
10、若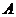 为不等式组
为不等式组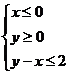 表示的平面区域,则当
表示的平面区域,则当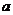 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线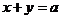 扫过
扫过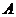 中的那部分区域的面积为
( )
中的那部分区域的面积为
( )
A.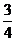 B.1 C.
B.1 C.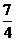 D.5
D.5
11、若直线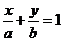 通过点
通过点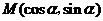 ,则( )
,则( )
A.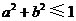 B.
B.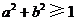 C.
C.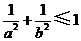 D.
D.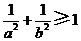
12、已知函数: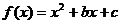 ,其中:
,其中: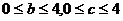 ,记函数
,记函数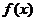 满足条件:
满足条件: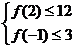 的事件为A,则事件A发生的概率为( )
的事件为A,则事件A发生的概率为( )
(A)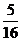 (B)
(B)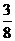 (C)
(C)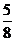 (D)
(D)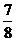
二、填空题
13、集合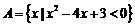 ,
,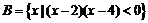 ,则
,则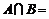 .
.
14、已知 ,
,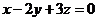 ,则
,则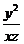 的最小值
.
的最小值
.
15、设变量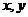 满足约束条件
满足约束条件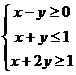 ,则目标函数
,则目标函数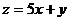 的最大值为___
的最大值为___
16、若不等式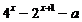 ≥0在[1,2]上恒成立,则a的取值范围为 .
≥0在[1,2]上恒成立,则a的取值范围为 .
三、解答题
17、记关于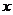 的不等式
的不等式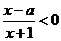 的解集为
的解集为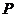 ,不等式
,不等式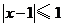 的解集为
的解集为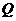 .
.
(I)若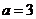 ,求
,求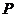 ;(II)若
;(II)若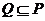 ,求正数
,求正数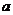 的取值范围.
的取值范围.
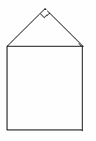 18、如图,某单位用木料制作如图所示的框架,框架的下部是边长分别为
18、如图,某单位用木料制作如图所示的框架,框架的下部是边长分别为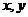 (单位:米)的矩形,上部是斜边长为
(单位:米)的矩形,上部是斜边长为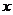 的等腰直角三角形,要求框架围成的总面积为8平方米.
的等腰直角三角形,要求框架围成的总面积为8平方米.
(Ⅰ)求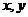 的关系式,并求
的关系式,并求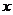 的取值范围;
的取值范围;
(Ⅱ)问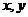 分别为多少时用料最省?
分别为多少时用料最省?
 19、某物流公司购买了一块长
19、某物流公司购买了一块长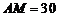 米,宽
米,宽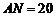 米的矩形地块
米的矩形地块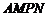 ,规划建设占地如图中矩形
,规划建设占地如图中矩形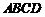 的仓库,其余地方为道路和停车场,要求顶点
的仓库,其余地方为道路和停车场,要求顶点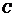 在地块对角线
在地块对角线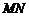 上,
上,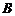 、
、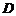 分别在边
分别在边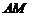 、
、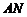 上,假设
上,假设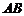 长度为
长度为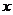 米.(1)要使仓库占地
米.(1)要使仓库占地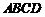 的面积不少于144平方米,
的面积不少于144平方米,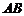 长度应在什么范围内?
长度应在什么范围内?
(2)若规划建设的仓库是高度与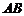 长度相同的长方体形建筑,问
长度相同的长方体形建筑,问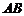 长度为多少时仓库的库容最大?(墙体及楼板所占空间忽略不计)
长度为多少时仓库的库容最大?(墙体及楼板所占空间忽略不计)
20、某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备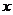 年的年平均污水处理费用
年的年平均污水处理费用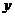 (万元);
(万元);
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水
处理设备?
21、命题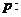 实数
实数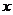 满足
满足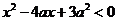 ,其中
,其中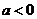 ,命题
,命题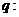 实数
实数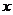 满足
满足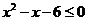 或
或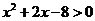 ,且
,且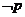 是
是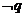 的必要不充分条件,求
的必要不充分条件,求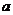 的取值范围.
的取值范围.
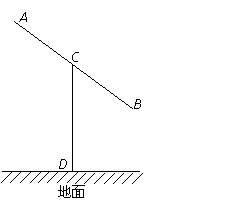 22、某建筑的金属支架如图所示,根据要求
22、某建筑的金属支架如图所示,根据要求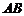 至少长2.8m,
至少长2.8m,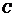 为
为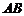 的中点,
的中点,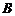 到
到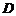 的距离比
的距离比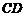 的长小0.5m,
的长小0.5m,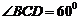 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计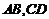 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
B
C
A
B
D
A
D
B
A
C
D
C
1、B
解: -
- =
= ,
, -
- =
= ,
, <
< ,故(A)错。
,故(A)错。
( +
+ )2=8+2
)2=8+2 ,(
,( +
+ )2=8+2
)2=8+2 ,故(B)对。
,故(B)对。
( +
+ )2=20+
)2=20+ ,(3+
,(3+ )2=20+
)2=20+ ,故(C)错。
,故(C)错。
5+ <5+
<5+ =8,故(D)也错。
=8,故(D)也错。
2、C
解:由 ,得
,得 ,即,-2<x-1<1,即-1<x<2,又x
,即,-2<x-1<1,即-1<x<2,又x Z,所以x为0,1,即N={0,1},故可选(C)。
Z,所以x为0,1,即N={0,1},故可选(C)。
3、A
解: =-
=- -2<0,故①错;
-2<0,故①错;
 =
= ≥0,故②对;
≥0,故②对;
 =
= ,因为
,因为 ,b符号不确定,故③不一定成立。
,b符号不确定,故③不一定成立。
对于④,因为a,b的符号不确定,也不成立。
4、B
解:当a,b都大于0时,由 ,得a≥b,所以,有
,得a≥b,所以,有 成立,
成立,
当a,b都小于0时,由 ,得a≤b,所以,有
,得a≤b,所以,有 成立,必要性成立。
成立,必要性成立。
而当a<b,且b<0时, 成立,
成立, 不成立,充分性不成立。
不成立,充分性不成立。
5、D
解:当x=0时,原不等式为 +4≥0显然成立,当x=2时,原不等式为
+4≥0显然成立,当x=2时,原不等式为 +4≥2
+4≥2 +2,即
+2,即 -2
-2 +2≥0,即(k2-1)2+1≥0,也成立,故选(D)。
+2≥0,即(k2-1)2+1≥0,也成立,故选(D)。
6、A
解:由x(3-x)>0,得x2-3x<0,解得:0<x<3。
7、D
解:由 ,且
,且 ,∴
,∴ ,∴
,∴
 。
。
8、B
解:依题意,有 ,解得:
,解得: ,f(x)=
,f(x)= ,
,
f(-x)= ,开口向下,与x轴交点为2,-1,对称轴为x=
,开口向下,与x轴交点为2,-1,对称轴为x=
9、A
解:依题意,直线经过圆的圆心,圆心为(-1,2),故有-2a-2b+2=0,即a+b=1,

 =
= =
= ≥
≥ =4
=4
10、C
解:如图知区域的面积是△OAB去掉一个小直角三角形。
(阴影部分面积比1大,比 小,故选C,不需要算出来)
小,故选C,不需要算出来)
11、D.由题意知直线 与圆
与圆 有交点,则
有交点,则 .
.
另解:设向量 ,由题意知
,由题意知
由 可得
可得
12、C
解:由 ,可得:
,可得:
知满足事件A的区域:的面积 10,而满足所有条件的区域
10,而满足所有条件的区域 的面积:
的面积: ,从而,得:
,从而,得: 。
。
二、填空题
13、
解:A= ,B=
,B= ,可求
,可求 。
。
14、3
 解:由
解:由 得
得 ,代入
,代入 得
得 ,当且仅当
,当且仅当 =3
=3 时取“=”.
时取“=”.
15、5
解:如图,由图象可知目标函数 过点
过点 时
时
 取得最大值,
取得最大值, ,
,
16、a≤0.
解:a≤ 在[1,2]上恒成立,a≤(
在[1,2]上恒成立,a≤( )min=(
)min=( )min=0.
)min=0.
三、解答题
17、解:(I)由 ,得
,得 .
.
(II) .
.
由 ,得
,得 ,又
,又 ,所以
,所以 ,
,
即 的取值范围是
的取值范围是 .
.
18.解:(Ⅰ)由题意得:


(Ⅱ)设框架用料长度为 ,
,
则


当且仅当
 满足
满足
答:当  米,
米, 米时,用料最少.
米时,用料最少.
19、解:(1)依题意三角形NDC与三角形NAM相似,
所以 ,即
,即 ,
,  ,
,
矩形ABCD的面积为 ,定义域为
,定义域为 ,
,
要使仓库占地ABCD的面积不少于144平方米即 ,
,
化简得 ,解得
,解得 所以AB长度应在
所以AB长度应在 内.
内.
(2)仓库体积为
 得
得 ,
,
当 时
时 ,当
,当 时
时 所以
所以 时V取最大值
时V取最大值 米3,
米3,
即AB长度为20米时仓库的库容最大.
20、解:(1)
即 (
( );
);
(2)由均值不等式得:
 (万元)
(万元)
当且仅当 ,即
,即 时取到等号.
时取到等号.
答:该企业10年后需要重新更换新设备.
21、设
 ,
,


 =
=
因为 是
是 的必要不充分条件,所以
的必要不充分条件,所以

 ,且
,且 推不出
推不出
而 ,
,
所以 ,则
,则
即
22、解:设
连结BD.
则在 中,
中,


设
则
等号成立时
答:当 时,建造这个支架的成本最低.
时,建造这个支架的成本最低.