2006年临安市初中毕业考试
数学试卷
一、选择题(本题有15个小题,每小题3分,共45分)下面每小题给出的四个选项中,有且只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内。
1.如果a与-2互为相反数,那么a等于( )
A.-2 B.2
C.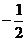 D.
D.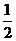
2.小明从正面观察下图所示的两个物体,看到的是( )
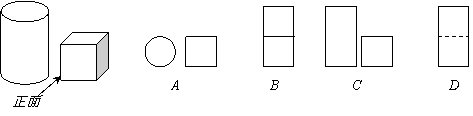 |
3.我市2005年的最高气温为
A.(+39)-(-7) B.(+39)+(+7) C.(+39)+(-7) D.(+39)-(+7)
4.化简的结果是 ( )
A.-2 B.±2 C.2 D.4
5.下列各式计算正确的是( )。
A.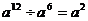 ; B.
; B.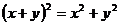 ; C.
; C.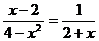 ; D.
; D.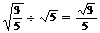 。
。
6.抛物线y=3(x-1) +1的顶点坐标是( )
+1的顶点坐标是( )
A.(1,1) B.(-1,1) C.(-1,-1) D.(1,-1)
 7.如图,正方形硬纸片ABCD的边长
7.如图,正方形硬纸片ABCD的边长
是4,点E、F分别是AB、BC的中点,
若沿左图中的虚线剪开,拼成如下右图
的一座“小别墅”,则图中阴影部分的
面积是( )。
A.2 B.4 C.8 D.10
8.某青年排球队12名队员的年龄情况如下:
年龄(单位:岁)
18
19
20
21
22
人 数
1
4
3
2
2
则这个队队员年龄的众数和中位数是 ( )
A.19,20 B.19,19 C.19,20.5 D.20,19
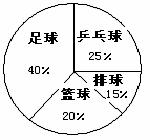 9.某校九(1)班的全体同学最喜欢的球类运动用图所示的统计图来表示,下面说法正确的是( )
9.某校九(1)班的全体同学最喜欢的球类运动用图所示的统计图来表示,下面说法正确的是( )
A.从图中可以直接看出喜欢各种球类的具体人数;
B.从图中可以直接看出全班的总人数;
C.从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况;
D.从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系。
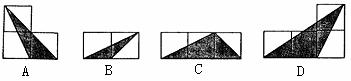
 10.如图,小正方形的边长均为l,则下列图中的三角形(阴影部分)与△ABC相似的是( )。
10.如图,小正方形的边长均为l,则下列图中的三角形(阴影部分)与△ABC相似的是( )。
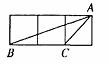
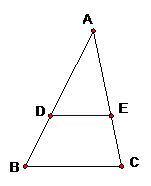
11. 如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE∶BC的值为( )
A.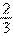 B.
B.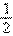 C.
C.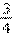 D.
D.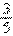
12.10名学生的平均成绩是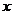 ,如果另外5名学生每人得84分,那么整个组的平均成绩是( )
,如果另外5名学生每人得84分,那么整个组的平均成绩是( )
 A.
A.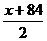 B.
B.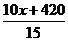 C.
C.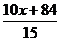 D.
D.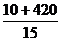
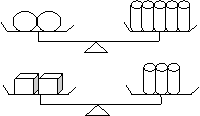
13.中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.
A.2 B
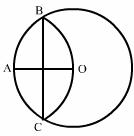 14.如图, ⊙O的半径OA=6, 以A为圆心,OA为半径的弧交⊙O于B、C两点, 则BC= ( )
14.如图, ⊙O的半径OA=6, 以A为圆心,OA为半径的弧交⊙O于B、C两点, 则BC= ( )
A. 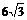 B.
B.
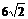 C.
C.
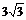 D.
D.
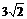
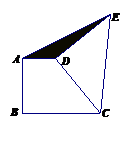 15.如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是 ( )
15.如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是 ( )
A.1 B.
二、填空题(本题有5个小题,每小题3分,共15分)
16.P(3,-4)到x轴的距离是 .
 17.用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=
度.
17.用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=
度.

18.为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有10条,则估计池塘里有鱼______________条.
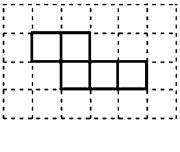 19.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示.)
19.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示.)
20.已知: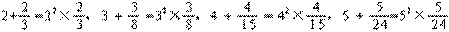 , ……,若
, ……,若 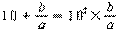 符合前面式子的规律, 则 a + b = ___ ____.
符合前面式子的规律, 则 a + b = ___ ____.
三、解答题(本题有6个小题,共40分)解答应写出文字说明,证明过程或推演步骤
21.(本题满分6分)
(1)化简÷(x-).
(2)解方程: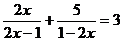 。
。
解:
已知a、b、c为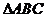 的三边,且满足
的三边,且满足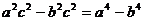 ,试判断
,试判断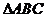 的形状。
的形状。
解: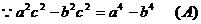
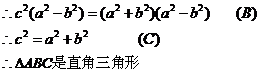
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号: ;
(2)错误的原因为: ;
(3)本题正确的结论为:
23. (本题满分7分)
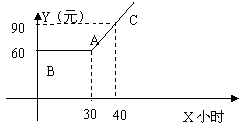
某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如右下图所示,其中BA是线段,且BA∥x轴,AC是射线。
(1)当x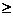 30,求y与x之间的函数关系式;
30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
 |
24.(本题满分7分)不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为.
(1)试求袋中蓝球的个数.
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.
25.(本题满分6分)已知:如图,E、F是平行四边行ABCD的对角线AC上的两点,AE=CF。
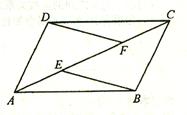 求证:(1)△ADF≌△CBE;
求证:(1)△ADF≌△CBE;
(2)EB∥DF。
26.(本小题8分)
如图,△OAB是边长为 的等边三角形,其中O是坐标原点,顶点B在
的等边三角形,其中O是坐标原点,顶点B在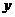 轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E//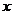 轴时,求点A′和E的坐标;
轴时,求点A′和E的坐标;
(2)当A′E//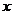 轴,且抛物线
轴,且抛物线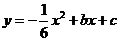 经过点A′和E时,求抛物线与
经过点A′和E时,求抛物线与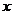 轴的交点的坐标;
轴的交点的坐标;
(1) 当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.

2006年临安市初中毕业考试
一.选择题:(本大题共15个题;每小题3分,共45分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案
B
C
A
C
D
A
B
A
D
B
A
B
D
A
A
 二.填空题:(本大题共5小题;每小题3分,共15分。)
二.填空题:(本大题共5小题;每小题3分,共15分。)
16.4 17. 36 ; 18. 20000; 19.
20.109
三.解答题:(本大题共6小题,共40分。解答应写出文字说明、证明过程或演算步骤。)
21.
解:(1)原式 ---1分
---1分
 ---2分
---2分
 ---3分
---3分
(2)
解:去分母得2x-5=3(2x-1)
即2x-5=6x-3---1分
∴4x=-2
x= ---2分
---2分
当x= 时,2x-1≠0
时,2x-1≠0
所以x= 是原方程的解---3分
是原方程的解---3分
22.(本题6分)
(1) C ---2分
(2)没有考虑 ---4分
---4分
(3) ---6分
---6分
23.(本题7分)
解(1)当x 30时,设函数关系式为y=kx+b
30时,设函数关系式为y=kx+b
则 -------2分
-------2分
解得
所以y=3x-30-------4分
(2)4月份上网20小时,应付上网费60元-------5分
(3) 由75=3x-30解得x=35,所以5月份上网35个小时. -------7分
24.(本题7分)
解:⑴设蓝球个数为 个
-------1分
个
-------1分
则由题意得 -------2分
-------2分

 答:蓝球有1个
--------3分
答:蓝球有1个
--------3分
--------4分
---------5分
∴ 两次摸到都是白球的概率 =
= ----------7分
----------7分
 25.(本题6分)
25.(本题6分)
证明:(1)∵AE=CF
∴AE+EF=CF+FE即AF=CE --------- 1分
又ABCD是平行四边形,∴AD=CB,AD∥BC
∴∠DAF=∠BCE ---------2分
在△ADF与△CBE中
 ---------3分
---------3分
∴△ADF≌△CBE(SAS)---------4分
(2)∵△ADF≌△CBE
∴∠DFA=∠BEC ---------5分
∴DF∥EB---------6分
26.(本题8分)
(1)由已知可得∠A,OE=60o , A,E=AE
由A′E// 轴,得△OA,E是直角三角形,
轴,得△OA,E是直角三角形,
设A,的坐标为(0,b)
AE=A,E= ,OE=2b
,OE=2b

所以b=1,A,、E的坐标分别是(0,1)与( ,1) --------3分
,1) --------3分
(2) 因为A,、E在抛物线上,所以

所以 ,函数关系式为
,函数关系式为
由 得
得
与x轴的两个交点坐标分别是( ,0)与(
,0)与( ,0)--------6分
,0)--------6分
(3) 不可能使△A′EF成为直角三角形。
∵∠FA,E=∠FAE=60o,若△A′EF成为直角三角形,只能是∠A,EF=90o或∠A,FE=90o
若∠A,EF=90o,利用对称性,则∠AEF=90o, A,、E、A三点共线,O与A重合,与已知矛盾;
同理若∠A,FE=90o也不可能
所以不能使△A′EF成为直角三角形。--------8分