浙江省2006年初中毕业生学业水平考试(金华卷)
数学试卷
考生须知:
1.全卷共三大题,24小题,满分为150分。考试时间为100分钟。本次考试采用开卷形式。
2.全卷分试卷Ⅰ(选择题)和试卷Ⅱ(非选择题)两部分。试卷Ⅰ的答案必须填涂在“答题卡”上;试卷Ⅱ的答案必须做在“试卷Ⅱ答题卷”的相应位置上。
3.请用钢笔或圆珠笔在“答题卡”上先填写姓名和准考证号,再用2B铅笔将准考证号和考试科目对应的方框涂黑、涂满。
4.用钢笔或圆珠笔在“试卷Ⅱ答题卷”密封区内填写县(市、区)、学校、姓名和准考证号。
试 卷 Ⅰ
说明:
本卷共有一大题,10小题,共40分。请用2B铅笔在“答题卡”上将所选项对应字母的方框涂黑、涂满。
一、选择题(本题共10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选均不给分)
1. 当 =1时,代数式2
=1时,代数式2 +5的值为( ▲ )
+5的值为( ▲ )
A.3 B. 5 C. 7 D. -2
2.直角坐标系中,点P(1,4)在( ▲ )
A. 第一象限 B.第二象限 C.第三象限 D.第四象限
3.我省各级人民政府非常关注“三农问题”.截止到2005年底,我省农村居民人均纯收入已连续二十一年位居全国各省区首位,据省统计局公布的数据,2005年底我省农村居民人均收入约6600元,用科学记数法表示应记为( ▲ )
A.0.66×104 B. 6.6×103 C.66×102 D .6.6×104
 4.下图所示的几何体的主视图是(
▲ )
4.下图所示的几何体的主视图是(
▲ )
A. B. C. D.
5.下列四幅图形中,表示两颗小树在同一时刻阳光下的影子的图形可能是( ▲ )

A. B. C. D.
6.如果两圆半径分别为3和4,圆心距为7,那么两圆位置关系是( ▲ )
A. 相离 B. 外切 C. 内切 D.相交
7.不等式组
 的解是( ▲ )
的解是( ▲ )
A. -2 ≤ ≤2
B.
≤2
B.  ≤2 C.
≤2 C.  ≥-2 D.
≥-2 D.  <2
<2
8.将叶片图案旋转180°后,得到的图形是( ▲ )

叶片图案 A B C D
9.下图能说明∠1>∠2的是( ▲ )

A B C D
 10.二次函数
10.二次函数 (
( )的图象如图所示,则下列结论:
)的图象如图所示,则下列结论:
① >0; ②
>0; ② >0; ③b2-4
>0; ③b2-4
 >0,
>0,
其中正确的个数是( ▲ )
A. 0个 B. 1个
C. 2个 D. 3个
试 卷 Ⅱ
说明:
本卷共有两大题,14小题,共110分。请用蓝(黑)色墨水钢笔或圆珠笔将答案写在“试卷Ⅱ答题卷”的相应位置上。
二、填空题 (本题有6小题,每题5分,共30分)
11.在函数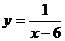 的表达式中,自变量
的表达式中,自变量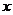 的取值范围是 ▲ .
的取值范围是 ▲ .
12.分解因式:2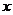 2+4
2+4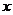 +2= ▲ .
+2= ▲ .
13.一射击运动员在一次射击练习中打出的成绩如下表所示:
 这次成绩的众数是 ▲ .
这次成绩的众数是 ▲ .
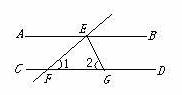
 14.如图,已知AB∥CD,直线EF分别交 AB、CD于点
E,F,EG平分∠BEF交CD于点G,如果∠1=50°,那么∠2的度数是 ▲ 度.
14.如图,已知AB∥CD,直线EF分别交 AB、CD于点
E,F,EG平分∠BEF交CD于点G,如果∠1=50°,那么∠2的度数是 ▲ 度.
第14题 第15题 第16题
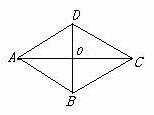
15.如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为 ▲ .
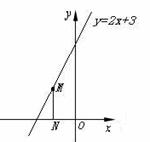
16.如图,点M是直线y=2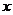 +3上的动点,过点M作MN垂直于
+3上的动点,过点M作MN垂直于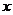 轴于点N,
轴于点N,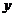 轴上是否存在点P,使△MNP为等腰直角三角形.小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形.那么,在y轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标 ▲ .
轴上是否存在点P,使△MNP为等腰直角三角形.小明发现:当动点M运动到(-1,1)时,y轴上存在点P(0,1),此时有MN=MP,能使△NMP为等腰直角三角形.那么,在y轴和直线上是否还存在符合条件的点P和点M呢?请你写出其它符合条件的点P的坐标 ▲ .
三、解答题 (本题有8小题,共80分,各小题都必须写出解答过程)
17.(本题8分)
(1)计算: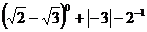 . (2)解方程:
. (2)解方程: 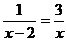 .
.
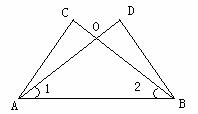 18.(本题8分)
18.(本题8分)
如图,△ABC与△ABD中, AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是: ▲ .
证明:
19.(本题8分)
北京08奥运会吉祥物是“贝贝、晶晶、欢欢、迎迎、妮妮”.现将三张分别印有“欢欢、迎迎、妮妮”这三个吉祥物图案的卡片(卡片的形状大小一样,质地相同)放入盒子.

(1)小玲从盒子中任取一张,取到卡片欢欢的概率是多少?
(2)小玲从盒子中取出一张卡片,记下名字后放回,再从盒子中取出第二张卡片,记下名字.用列表或画树状图列出小玲取到的卡片的所有可能情况,并求出两次都取到卡片欢欢的概率.
20.(本题8分)
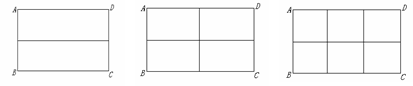
现有9个相同的小正三角形拼成的大正三角形,将其部分涂黑.如图(1),(2)所示.
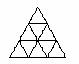
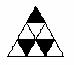

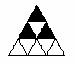
图(1) 图(2) 图(3) 图(4)
观察图(1),图(2)中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形②涂黑部分都是三个小正三角形.
请在图(3),图(4)内分别设计一个新图案,使图案具有上述两个特征.
21.(本题10分)
|
 m, 设AB为
m, 设AB为 经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在
经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在 m共有n条竖档时, 那么当竖档AB多少时,
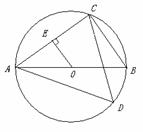
m共有n条竖档时, 那么当竖档AB多少时,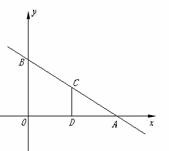 如图,平面直角坐标系中,直线AB与
如图,平面直角坐标系中,直线AB与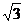 )两点, ,点C为线段AB上的一动点,过点C作CD⊥
)两点, ,点C为线段AB上的一动点,过点C作CD⊥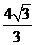 ,求点C的坐标;
,求点C的坐标; ; 13.8;
14. 65°;
; 13.8;
14. 65°;  ),(0,-3)写对一个给3分,两个4分,三个给5分
),(0,-3)写对一个给3分,两个4分,三个给5分 …………(3分)
…………(3分) …………(1分)
…………(1分) ; …………(3分)
; …………(3分) . …………(2分)
. …………(2分) . ………(3分)
. ………(3分) . …(3分)
. …(3分) =4, ∴tan∠ADC= tan∠ABC=
=4, ∴tan∠ADC= tan∠ABC= .
……(2分)
.
……(2分) ; (每格2分)
……………(6分)
; (每格2分)
……………(6分)
 . ……………(2分)
. ……………(2分) 时,S最大. ……………(2分)
时,S最大. ……………(2分) x+
x+ .
……………(3分)
.
……………(3分) =
= =
= .
………(2分)
.
………(2分) ,解得
,解得 (舍去) ………(2分)
(舍去) ………(2分) ) ………(1分)
) ………(1分) ,
, .…(2分)
.…(2分) =
= =
= .可得CD=
.可得CD= ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2, (3,
(3, (1,
(1, 过点P作PM⊥OA于点M.
过点P作PM⊥OA于点M. ,OP=
,OP= .∴
.∴ (
( 方法二:设P(x ,
方法二:设P(x , =
= ,tan∠ABOC=
,tan∠ABOC= =
= .
. (
(