1．计算：2+(-3)的结果是(▲)

  A.-l    B．1    C．-5    D．5

2．在下列几何体中,主视图是圆的是(▲)

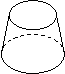
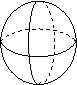
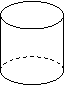
      A                B              C            D

3．如图,AB是⊙0的直径，点C在⊙0上，么B=70°，则∠A的度数是(  ▲)

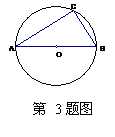  A.20°    B．25°  C．30°    D．35°

4．反比例函数y= 的图象经过点(-1,2)，k的值是(▲)

A.-          B.         C.-2        D.2

5．点A(1,2)向右平移2个单位得刊对应点A’,则点A’的坐标是(▲)

 A.(1．4)   B.(1．0)  C．(-l，2)    D.(3，2)

6．在一个暗箱里,装有3个红球、5个黄璋和7个绿球，它们除颜色外都相同,搅拌均匀后，从中任意摸出一个球是红球的概率是(▲)

A.     B.     C.     D.

7．方程，x­­_­­­²-9=0的解是(▲)

  A．x_l=x₂=3       B. x_l=x₂=9

  C．x_l=3,x₂=-3    D. x_l=9,x₂=-9

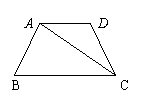
8．如图，在梯形ABCD中,AD∥BC,CA平分么BCD,CD=5，则AD的长是(▲)

A.6    B.5     C. 4     D. 3

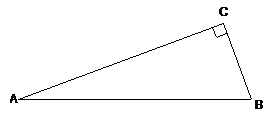
9．如图,在△ABC中,∠C=90°,

BC=5,AC=12,则 cosA等于(▲)

A.     B.    

C.     D.

10．晓晓根据下表，作了三个推测：

x

  1

  lO

  100

  1000

  10000

…

 3-

    3

    2.1

  2．Ol

  2.001

 2.0001

…

   ①3- (x>0)的值随着I的增大越来越小；

   ②3- (x>0)的值有可能等于2；

   ③3-  (x>O)的值随着x的增大越来越接近于2．

   则推测正确的有(▲)

    A.0个    B.1个    C．2个    D. 3个

卷    二

1．若x-y=3，则2x-2y=         ．

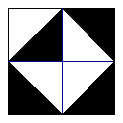
12.右图是由8块相同的等腰直角三角形黑白瓷砖镶嵌而成的正方形地面示意图，一只蚂蚁在上面自由爬动,并随机停留在某块瓷砖上,尉蚂蚁停留在黑色瓷砖上的概率是      ．

13．二次函数y=2x²-4x+5的量小值是               ．

14.已知∠ABC=60°,点0在∠ABC的平分线上，OB＝5cm，以0为圆心3cm为半径作圆，则⊙0与BC的位置关系是　　　　　．

15.在边长为l的正方形网格中，按下列方式得到“L”形图形第1个“L”形图形的周长是8，第2个“L”形图形的周长是12，  则第n个“L”形图形的周长是              .

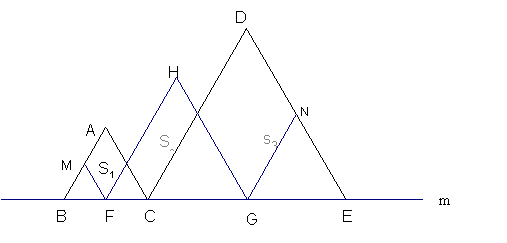16如图，在直线m上摆故着三个正三角形:△ABC、△HFG、△DCE,已知BC=CE,F、G分别是BC、CE的中点，FM∥AC，GN∥DC．设图中三个平行四边形的面积依次是S₁,S₂,S₃,若S₁+S₃=10，则S₂=       .

17(本题10分)(1)(-1)⁰+2sin30°+ ()²;

(2)计算：+;

18(本题8分)如图，点D、C在BF上，AB∥EF，∠A=∠E，BC=DF，

  求证AB=EF．

19.(本题10分)某公司欲招聘一名部门经理，对甲、乙两名候选人进行笔试和面试考核，甲、乙两人的笔试成绩分别是95分和93分，他们的面试成绩如下表：

(1)分别求出甲、乙两人面试成绩的平均分;

(2)公司决定笔试成绩的40％与面试成绩的平均分的60％的和作为综合成绩-综合成绩高者将被录用请你通过计算判断谁将被录用.

候选人

评委１

评委２

评委３

评委４

评委５

甲

乙

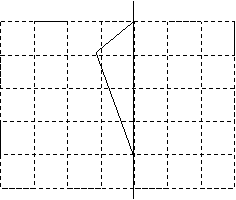
20(本题8分)请按下列要求画图:

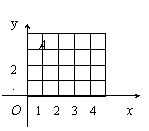
  (1)在图l中,直线m是一个轴对称围形的对称轴，画出这个轴对称图形的另一半;

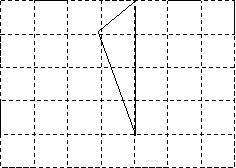
 (2)在囝2中，将三角形绕点,按雁时针方向旋转90°，画出旋转后的图形.

2l_(本题8分)矩形的周长是8cm设一边长为xcm,另一边长为ycm.

  (1)求y关于x的函数关系式，并写出自变量x的取值范围；(2)作出函数图象.

22(本题lO分)下图是A、B两所学校艺术节期间收到的各类艺术作品情况的统计图：

    (1)从图中休能否看出哪所学校收到的水粉画作品的数量多？为什么?

    (2)已知A学校收到的剪纸作品比B学校的多20件，收到的书法作品比B学校的少100件，请问这两所学校收到艺木作品的总数分别是多少件？

23(本题12分)下图是B、C两市到A市的公路示意图，小明和小王提供如下信息:

  小明：普通公路EA与高速公路DA的路程相等；

  小王：A、B两市的路程(B--D--A)为240千米，A、c两市的路程(C--E--A)为290千米，

  小明汽车在普通公路BD上行驶的平均速度是30千米／时，在高速公路DA上行驶的平均速度是90千米／时;

  小王汽车在高速公路CE上行驶的平均速度是lOO千米／时，在普通公路EA上行驶的平均速度是40千米／时；

小明汽车从B市到A市不超过5时；小王：汽车扶C市到A市也不超过5时.

    若设高速公路AD的路程为x千米.

(1)根据以上信息填表:

    路程

(单位千米)

    行驶速度

  (单位；千米／时)

  所需时间

  (单位时)

高速公路AD

普通公路BD

I普通公路AE

l高建公路CE

    (2)试确定高速公路AD的路程范围.

24(本题14分)如图，在   ABCD中，对角线AC⊥BC，AC=BC=2,动点P从点A出发沿AC向终点C移动，过点P分剐作PM∥AB交BC于M，PN∥AD交DC于N．连接AM．设AP=x

(1)四边形PMCN的形状有可能是菱形吗?请说明理由；

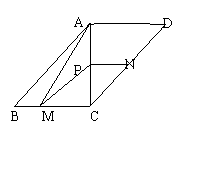(2)当x为何值时，四边形PMCN的面积与△ABM的面积相等?