南京市2OO6年初中毕业生学业考试
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分.第1卷1至2页,第Ⅱ卷3至8页.共120分.
考试时间120分钟.
第Ⅰ卷(选择题 共24分)
注意事项:
1.答第Ⅰ卷前考生务必将自己的准考证号、考试科目用2B铅笔填涂在答题卡上.
2.每小题选出答案后用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案.不能答在试卷上
下列各题所附的四个选项中,有且只有一个是正确的.
一、选择题(每小题2分,共24分)
1.如果 与
与 的和为O,那么
的和为O,那么 是-----------------------------------------( )
是-----------------------------------------( )
A.2 B.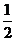 C.
C. D.
D.
2.计算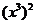 的结果是----------------------------------------------------( )
的结果是----------------------------------------------------( )
A.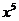 B.
B.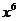 C.
C.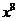 D.
D. 
3.去年南京市接待入境旅游者约876000人,这个数可以用科学记数法表示为----( ) A.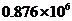 B.
B.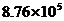 C.
C.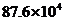 D.
D.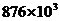
4.9的平方根是----------------------------------------------------------( )
A. 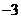 B.3 C.±3 D.81
B.3 C.±3 D.81
5.某地今年1月1日至4日每天的最高气温与最低气温如下表:
日 期
1月1日
1月2日
1月3日
1月4日
最高气温
5℃
4℃
0℃
4℃
最低气温
0℃
 ℃
℃
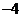 ℃
℃
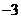 ℃
℃
其中温差最大的是------------------------------------------------------( )
A. 1月1日 B. 1月2日 C. 1月3日 D. 1月4日
6.其市气象局预报称:明天本市的降水概率为70%,这句话指的是------------( )
A. 明天本市70%的时间下雨,30%的时间不下雨
B. 明天本市70%的地区下雨,30%的地区不下雨
C. 明天本市一定下雨
D. 明天本市下雨的可能性是70%
7.下列图形中,是中心对称图形的是---------------------------------------( )
 A.菱形 B.等腰梯形 C.等边三角形 D.等腰直角三角形
A.菱形 B.等腰梯形 C.等边三角形 D.等腰直角三角形
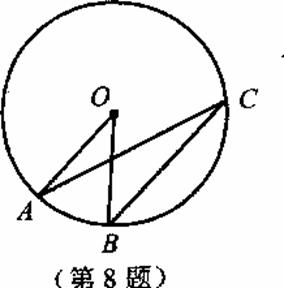
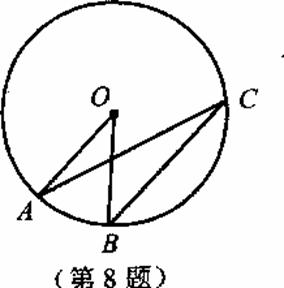

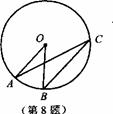
8.如图,点A、B、C在⊙O上,AO∥BC,∠OAC=20°,
则∠AOB的度数是------------------------------------( )
A.1O° B.20° C.40° D.70°
9.在△ABC中,∠C=90°,AB=2,AC=1,则Sin B的值是( )
A. 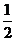 B.
B. 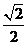 C.
C.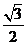 D.2
D.2
10.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,
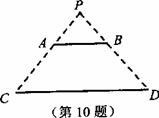 AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,
AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,
则P到AB的距离是-----------------------------( )
A.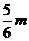 B.
B.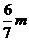
C.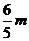 D.
D.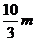
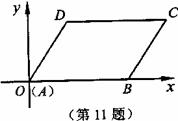 11.在平面直角坐标系中,□ABCD的顶点A、B、D
11.在平面直角坐标系中,□ABCD的顶点A、B、D
的坐标分别是(0,0),(5,0),(2,3),则顶点C的
坐标是--------------------------------( )
A.(3,7) B.(5,3)
C.(7,3) D.(8,2)
12.下面是两户居民家庭全年各项支出的统计图.
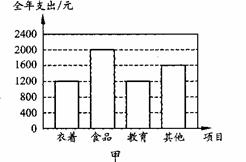
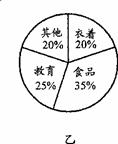
 根据统计图,下列对两户教育支出占全年总支出的百分比作出的判断中,正确的是( )
根据统计图,下列对两户教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大 B.乙户比甲户大
C.甲、乙两户一样大 D.无法确定哪一户大
南京市2OO6年初中毕业生学业考试
数 学
第 Ⅱ 卷( 共 9 6 分 )
小 计
题 号
二
三
四
五
六
七
八
得 分
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔(蓝色或黑色)直接答在试卷上.
2.答卷前将密封线内的项目及桌号填写清楚.
 二、填空题(每小题3分,共12分)
二、填空题(每小题3分,共12分)
13. 如图,在△ABC中,∠ABC=90°,∠A=50°,
BD∥AC,则∠CBD的度数是 °.
14.某种灯的使用寿命为1000小时,它的可使用天数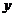 与平均
与平均
每天使用的小时数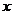 之间的关系式为 .
之间的关系式为 .
15.写出一个有理数和无理数,使它们都是大于 的负数:
.
的负数:
.
16.如图,矩形ABCD与与圆心在AB上的⊙O交于点G、B、F、E,
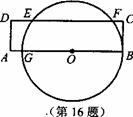 GB=8cm,AG=1cm,DE=2cm,则EF=
cm .
GB=8cm,AG=1cm,DE=2cm,则EF=
cm .
三、(每小题6分,共24分)
17.计算: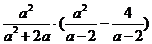 .
.
18.解不等式组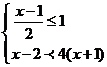 ,并写出不等式组的正整数解.
,并写出不等式组的正整数解.
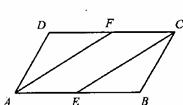 19. 已知:如图,□ABCD中,E、F分别是AB、CD的中点.
19. 已知:如图,□ABCD中,E、F分别是AB、CD的中点.
求证:(1)△AFD≌CEB;
(2)四边形AECF是平行四边形.
20.饮料店为了了解本店罐装饮料上半年的销售情况,随机调查了8天该种饮料的日销售量,结果如下(单位:听):33 ,32 ,28 ,32 ,25 ,24 ,31 ,35.
(1)这8天的平均日销售量是多少听?
(2)根据上面的计算结果,估计上半年(按181天计算)该店能销售这种饮料多少听?
四、(每小题6分,共12分)
21.某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.
现在停车场有50辆中、小型汽车,这些车共缴纳停车费230元,问中、小型汽车各有多少辆?
22.某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐.
(1)求甲、乙、丙三名学生在同一个餐厅用餐的概率;
(2)求甲、乙、丙三名学生中至少有一人在B餐厅用餐的概率.
五、(第23题7分,第24题8分,共15分)
23.在平面直角坐标系中,直线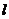 过点M(3,0),且平行于
过点M(3,0),且平行于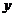 轴.
轴.
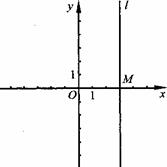 (1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-l,O),C(-1,2),△ABC关于
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-l,O),C(-1,2),△ABC关于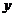 轴的对称图形是△A1B1C1,△A1B1C1关于直线
轴的对称图形是△A1B1C1,△A1B1C1关于直线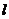 的对称
的对称
图形是△A2B2C1,写出△A2B2C1的三个顶点的坐标;
(2)如果点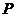 的坐标是(
的坐标是(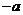 ,0),其中
,0),其中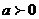 ,点P关于
,点P关于
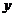 轴的对称点是
轴的对称点是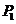 ,点
,点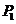 关于直线
关于直线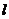 的对称点是
的对称点是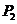 ,
,
求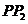 的长.
的长.
24.某块试验田里的农作物每天的需水量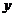 (千克)与生长时间
(千克)与生长时间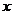 (天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
(1)分别求出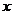 ≤40和
≤40和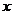 ≥40时
≥40时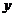 与
与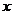 之间的关系式;
之间的关系式;
 (2)如果这些农作物每天的需水量大于或等于4000千克时
(2)如果这些农作物每天的需水量大于或等于4000千克时
需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
六、(每小题8分,共16分)
25.如图,在矩形ABCD中,AB=2AD,线段EF=10.在EF上取一点M,分别以EM、MF为
一边作矩形EMNH、矩形MFGN,使矩形MFGN∽矩形ABCD.令MN=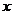 ,当
,当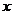 为何值时,矩形EMNH的面积S有最大值?最大值是多少?
为何值时,矩形EMNH的面积S有最大值?最大值是多少?
26.西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价O.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元.该经营户要想每天盈利2O0元,应将每千克小型西瓜的售价降低多少元?
七、(本题8分)
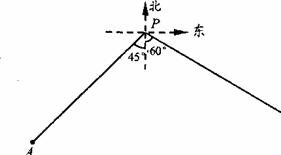
27.如图,小岛A在港口P的南偏西45°方向,距离港口8l海里处.甲船从A出发,
沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东6O°方向,
以l8海里/时的速度驶离港口.现两船同时出发,
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)
 (参考数据:
(参考数据: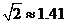 ,
,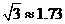 )
)
八、(本题9分)
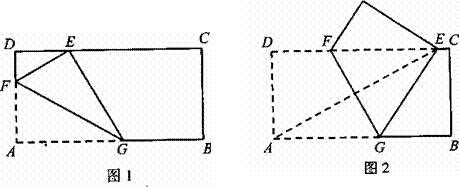
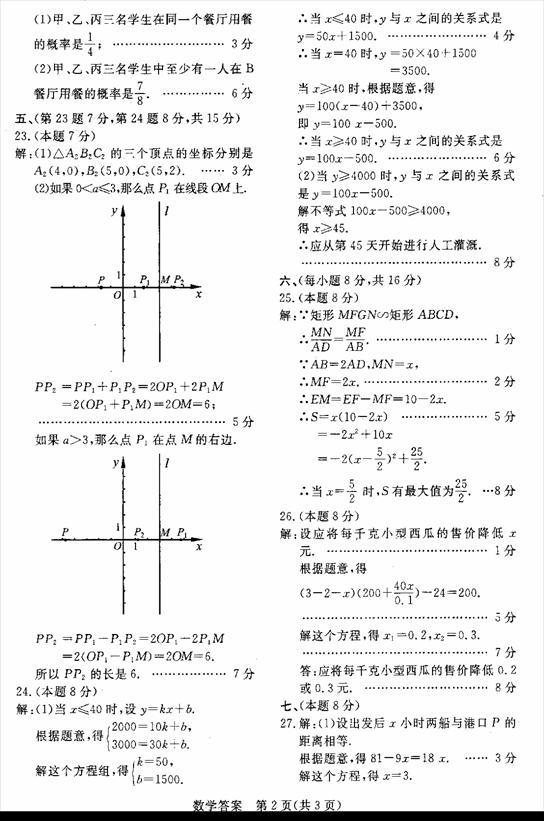
28.已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.
(1)如果折痕FG分别与AD、AB交与点F、G(如图1), ,求DE的长;
,求DE的长;
(2)如果折痕FG分别与CD、AB交与点F、G(如图2),△AED的外接圆与直线BC相切,
求折痕FG的长.