湖北省武汉市教科院2009届高三第一次调考数学理科
本试卷共150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷的答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。非选择题用黑色墨水的签字笔或钢笔直接答在答题卡上。答在试题卷上无效。
3.考试结束,监考人员将本试题和答题卡一并收回。
4.注明文科做的理科不做,注明理科做的文科不做。
参考公式:
如果事件A、B互斥,那么
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么
P(A?B)=P(A)?P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率

球的表面积公式

其中R表示球的半径
球的体积公式

其中R表示球的半径
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一次是符合题目要求的。
1.已知集合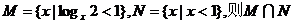 = ( )
= ( )
A.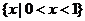 B.
B.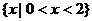 C.
C.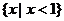 D.
D.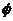
2.“p或q是假命题”是“非p为真命题”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3.双曲线 的两近渐近线和直线x=2围成一个三角形区域(含边界),则该区域可表示为 ( )
的两近渐近线和直线x=2围成一个三角形区域(含边界),则该区域可表示为 ( )
A.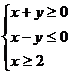 B.
B.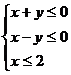 C.
C.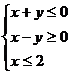 D.
D.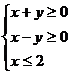
4.(文科)在等比数列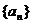 中,若
中,若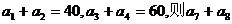 = ( )
= ( )
A.100 B.
(理科)已知Sn表示等差数列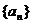 的前n项和,且
的前n项和,且 = ( )
= ( )
A.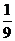 B.
B.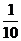 C.
C. D.
D.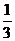
5.(文科)已知函数 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )
A.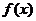 是周期为1的奇函数 B.
是周期为1的奇函数 B.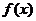 是周期为2的偶函数
是周期为2的偶函数
C.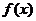 是周期为1的非奇非偶数 D.
是周期为1的非奇非偶数 D.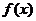 是周期为2的非奇非偶函数
是周期为2的非奇非偶函数
(理科)△ABC中, 的面积为 ( )
的面积为 ( )
A. B.
B. C.
C.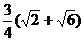 D.
D.
6.已知直线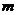 、
、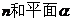 ,下列命题中的真命题是 ( )
,下列命题中的真命题是 ( )
A.如果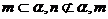 、
、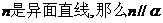 ;
;
B.如果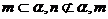 、
、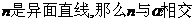 ;
;
C.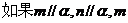 、
、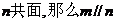 ;
;
D.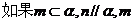 、
、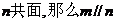 ;
;
7.已知 等于 ( )
等于 ( )
A.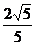 B.
B.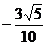 C.
C.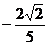 D.
D.
8.设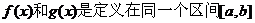 上的两个函数,若对任意的
上的两个函数,若对任意的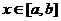 ,都有
,都有
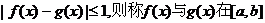 上是“密切函数”,[a,b]称为“密切区间”,设
上是“密切函数”,[a,b]称为“密切区间”,设 上是“密切函数”,则它的“密切区间”可以是 ( )
上是“密切函数”,则它的“密切区间”可以是 ( )
A.[1,4] B.[2,3] C.[3,4] D.[2,4]
9.(文科)若第一象限内的点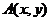 落在经过点(6,―2)且方向向量为
落在经过点(6,―2)且方向向量为 的直线
的直线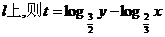 有 ( )
有 ( )
A.最大值 B.最大值
B.最大值 D.最小值1
D.最小值1
|
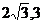 ) C.(0,4) D.(0,
) C.(0,4) D.(0,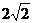 )
)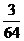 B.
B. C.
C. D.
D.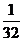
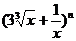 的展开式的各项系数的和为p,所有二项式系数的和为q,且p+q=272,则n的值为
。
的展开式的各项系数的和为p,所有二项式系数的和为q,且p+q=272,则n的值为
。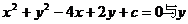 轴交于A、B两点,圆心为P,若
轴交于A、B两点,圆心为P,若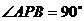 ,则c的值等于
。
,则c的值等于
。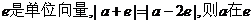 方向上的投影为 。
方向上的投影为 。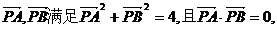 若向量
若向量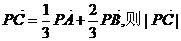 的最大值为 。
的最大值为 。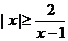 的解集为
。
的解集为
。 的取值范围是
。
的取值范围是
。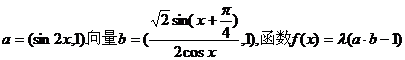
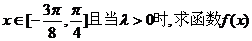 的单调递减区间;
的单调递减区间;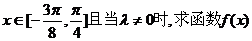 的单调递减区间;
的单调递减区间;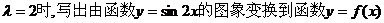 的图象的变换过程。
的图象的变换过程。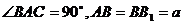 ,直线B
,直线B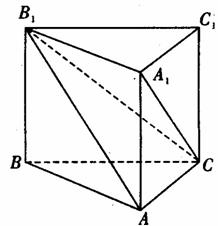
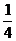 ,乙胜丙的概率为
,乙胜丙的概率为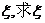 的分布列和数学期望。
的分布列和数学期望。
 的值;
的值; 是否存在最小值?若存在,求出
是否存在最小值?若存在,求出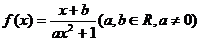 是奇函数,当且仅当
是奇函数,当且仅当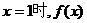 取得最大值。
取得最大值。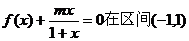 上有且仅有两个不同实根,求实数m的取值
上有且仅有两个不同实根,求实数m的取值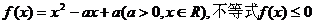 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列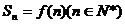
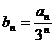 ,求数列
,求数列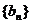 的前n项和Tn;
的前n项和Tn;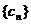 中,所有满足
中,所有满足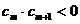 的正整数m的个数,称为这个数列
的正整数m的个数,称为这个数列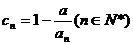 ,求数列
,求数列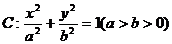 的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知
的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知
 (理)
(理)
 (理)
(理)





 …………(4分)
…………(4分) 时,
时,

 时,
时, 为减函数
为减函数 ;…………(文8分)
;…………(文8分) 时,函数的单调递减区间为
时,函数的单调递减区间为 …………(理8分)
…………(理8分) ,变换过程如下:
,变换过程如下: 的图象向右平移
的图象向右平移 个单位可得函数
个单位可得函数 的图象。
的图象。 倍,而横坐标保持不变,可得函数
倍,而横坐标保持不变,可得函数 的图象。
的图象。 的图象……(12分)
的图象……(12分) 三棱柱ABC―A1B
三棱柱ABC―A1B 底面ABC
底面ABC 面ABC
面ABC

 …………(6分)
…………(6分) 底面ABC
底面ABC 为直线B
为直线B



 …………(文12分)
…………(文12分) 知
知
 ………………(理12分)
………………(理12分) ………………………………(6分)
………………………………(6分) ……………………………………(12分)
……………………………………(12分) ………………………………………(6分)
………………………………………(6分) 可能的取值为0,3,6;则
可能的取值为0,3,6;则




 的分布列为
的分布列为 …………………………(12分)
…………………………(12分)


 …………………………………(6分)
…………………………………(6分) 、
、




 ……(13分)
……(13分)



 即
即

 …………………………………………………(6分)
…………………………………………………(6分)






 ……………(13分)
……………(13分) 的解集有且只有一个元素
的解集有且只有一个元素





 …………………………………(文6分,理5分)
…………………………………(文6分,理5分) ①
① ②
②
 …………………………………………(文13分,理10分)
…………………………………………(文13分,理10分)

 共有3个变号数,即变号数为3.……………………(理13分)
共有3个变号数,即变号数为3.……………………(理13分)

 ………………………………(文6分,理4分)(2)(2)当AB的斜率为0时,显然
………………………………(文6分,理4分)(2)(2)当AB的斜率为0时,显然 满足题意
满足题意 ,AB方程为
,AB方程为 代入椭圆方程
代入椭圆方程




 .………………………………(文13分,理9分)
.………………………………(文13分,理9分)