浙江省金华一中
2009届高三年级2月月考
数学试题(文科)
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合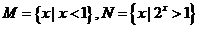 ,则
,则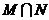 = ( )
= ( )
A.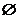 B.
B.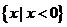 C.
C.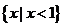 D.
D.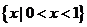
2.已知函数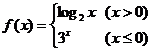 ,则
,则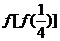 的值是 ( )
的值是 ( )
A.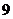 B.
B.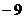 C.
C.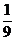 D.
D.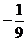
3.与不等式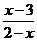 ≥0同解的不等式是 ( )
≥0同解的不等式是 ( )
A.(x-3)(2-x)≥0 B.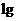 (x-2)≤
(x-2)≤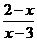 ≥0 D.(x - 3)(2 - x)>0
≥0 D.(x - 3)(2 - x)>0
4.如图是一个几何体的三视图,则这个几何体的体积是 ( )
A.27 B.
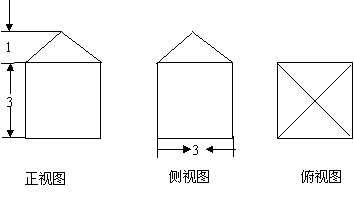
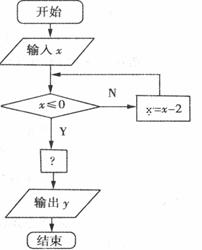 5.下面是一个算法的程序框图,当输入的
5.下面是一个算法的程序框图,当输入的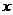 值为3时,
值为3时,
输出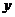 的结果恰好是
的结果恰好是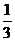 ,则?处的关系式是( ).
,则?处的关系式是( ).
A.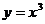
B.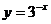
C.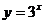
D.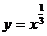
6.若曲线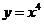 的一条切线
的一条切线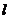 与直线
与直线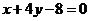
垂直,则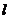 的方程为 ( )
的方程为 ( )
A.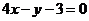 B.
B.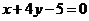

C.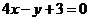 D.
D.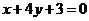

7.已知两个不同的平面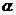 、
、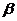 和两条不重合的直线,m、n,有下列四个命题
和两条不重合的直线,m、n,有下列四个命题
①若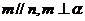 则
则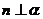 ②若
②若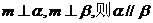
③若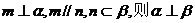 ④若
④若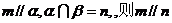
其中正确命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
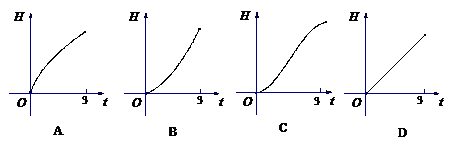
8.如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间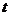 (分)的函数关系表示的图象只可能是 ( )
(分)的函数关系表示的图象只可能是 ( )

9.已知函数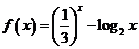 ,若实数
,若实数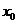 是方程
是方程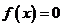 的解,且
的解,且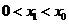 ,则
,则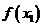 的值为 ( )
的值为 ( )
A.恒为正值 B.等于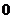 C.恒为负值 D.不大于
C.恒为负值 D.不大于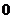
10.已知二次曲线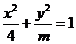 ,则当
,则当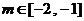 时,该曲线的离心率
时,该曲线的离心率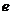 的取值范围是
的取值范围是 ( )
( )
A.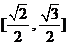 B.
B.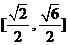
C.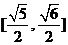 D.
D.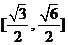

二、填空题(每小题4分,共28分)
11.复数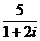 的共轭复数为________________。
的共轭复数为________________。
12.在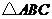 中,若
中,若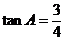 ,
,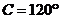 ,
,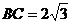 ,则
,则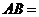 ________________。
________________。
13.一个容量为27的样本数据,分组后,组别与频数如下
组别
(10,20]
(20,30]
(30,40]
(40,50]
(50,60]
(60,70]
频数
2
3
4
5
6
7
则样本在(20,50)上的频率为 .
14.已知向量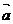 和
和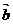 的夹角为120°,且|
的夹角为120°,且|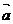 |=2,|
|=2,|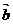 |=5,则(2
|=5,则(2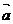 -
-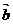 )?
)?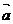 =_____
=_____
15.记等差数列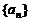 的前
的前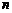 项和为
项和为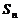 ,若
,若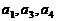 成等比数列,则
成等比数列,则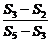 的值为 .
的值为 .
16.从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .
17.若实数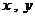 满足
满足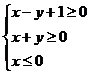 ,则
,则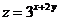 的最大值是_________________。
的最大值是_________________。
三、解答题:本大题共5小题,满分72分.解答须写出文字说明、证明过程和演算步骤.
18.(本题满分14分)函数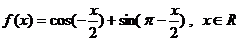 。
。
(1)求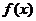 的周期;
的周期;
(2)求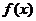 在
在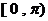 上的减区间;
上的减区间;
(3)若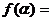
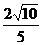 ,
,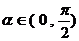 ,求
,求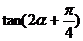 的值。
的值。
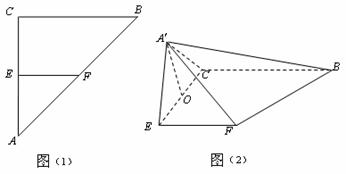
19.(本小题满分14分)如图(1),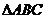 是等腰直角三角形,
是等腰直角三角形,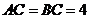 ,
, 、
、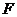 分别为
分别为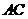 、
、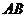 的中点,将
的中点,将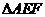 沿
沿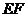 折起, 使
折起, 使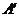 在平面
在平面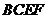 上的射影
上的射影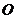 恰为
恰为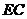 的中点,得到图(2).
的中点,得到图(2).
(Ⅰ)求证: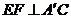 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
20.(本题满分14分)数列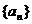 的前
的前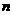 项和记为
项和记为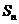 ,
,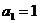 ,
,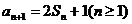 .
.
(1)求数列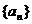 的通项公式;
的通项公式;
(2)等差数列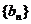 的前
的前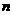 项和
项和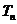 有最大值,且
有最大值,且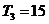 ,又
,又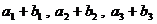 成等比数列,求
成等比数列,求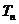 .
.
21.(本小题满分15分)设点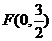 ,动圆
,动圆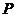 经过点
经过点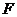 且和直线
且和直线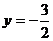 相切,记动圆的圆心
相切,记动圆的圆心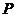 的轨迹为曲线
的轨迹为曲线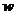 .
.
(1)求曲线 的方程
的方程
(2)过点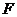 作互相垂直的直线
作互相垂直的直线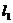 、
、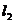 ,分别交曲线
,分别交曲线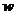 于
于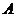 、
、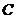 和
和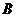 、
、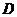 四个点,求四边形
四个点,求四边形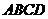 面积的最小值。
面积的最小值。
22.(本小题满分15分)已知实数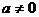 ,函数
,函数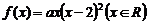 .
.
(I)若函数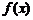 有极大值32,求实数
有极大值32,求实数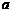 的值;
的值;
(II)若对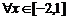 ,不等式
,不等式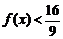 恒成立,求实数
恒成立,求实数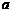 的取值范围.
的取值范围.
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
B
B
C
A
D
B
A
C
 二、填空题(每小题4分,共28分)
二、填空题(每小题4分,共28分)
11.1+2i
12.5
13.  14. 13
14. 13
15. 2或 16.
16.  17.9
17.9
三、解答题:本大题共5小题,满分72分.解答须写出文字说明、证明过程和演算步骤.
18.(本题满分14分)
解:(1)f(x)= T=4
T=4
(2) (3)
(3) 两边平方得
两边平方得
 ,而
,而 ∴
∴
 19.(本小题满分14分)
19.(本小题满分14分)
(1)证明:∵A/O⊥面CEFB
∴EF⊥A/O,又EF⊥EC
A/O∩EC=0
∴EF⊥面A/EC
而A/C 面A/EC
面A/EC
∴EF⊥A/C
(2)
20.(本题满分14分)
解:(1)an+1=2Sn+1,an=2Sn-1+1两式相减得an+1=3an(a≥2),又a2=2S1+1=
∴ {an}是以a1=1为首项,3为公比的等比数列,an=3n-1
{an}是以a1=1为首项,3为公比的等比数列,an=3n-1
(2)Tn= 5n2+20n
5n2+20n
21.(本小题满分15分)
解:(1)W:x2=6y
(2)设AC:
设A(x1,y1),C(x2,y2) |AC|=6(k2+1)
同理|BD|=6
SABCD=
当k=±1时取等号
22.(本小题满分15分)
解:(1)f(x)=ax3 4ax2+4ax
4ax2+4ax
f/(x)=3ax2 8ax+
8ax+ 2)(x
2)(x 2)=0
2)=0 x=
x= 或2
或2
∵f(x)有极大值32,而f(2)=0
∴f( )=32=7,a=27
)=32=7,a=27
(2)f/(x)=a(3x 2)(x
2)(x 2)
2)
当a>0时,f(x)=[  2,
2, ]上递增在[
]上递增在[ ]上递减,
]上递减,
 ∴0<a<
∴0<a<
当a<0时,f(x)在[ 2,
2, ]上递减,在[
]上递减,在[ ]上递增
]上递增
f( 2)=
2)= 
 ∴
∴
综上