福建省建瓯一中2009届高三第三次调研考试
数 学 试 题(理科)
命题 詹振照 审题 黄翠珍
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),全卷满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共50分)
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的4个选项中,只有一项是符合题目要求的,请将正确的选项填写到答题卷相应位置)
1.定义集合运算: ,设
,设 ,则集合
,则集合 的真子集个数为
(
)
的真子集个数为
(
)
A. B.
B. C.
C. D.
D.
2.下列命题错误的是 ( )
A.命题“若 ,则
,则 “的逆否命题为”若
“的逆否命题为”若 “
“
B.若命题 ,则
,则
C.若 为假命题,则
为假命题,则 ,
, 均为假命题
均为假命题
D. 的充分不必要条件
的充分不必要条件
3.若复数 是虚数单位),且
是虚数单位),且 是纯虚数,则
是纯虚数,则 等于 ( )
等于 ( )
A.40 B. C.
C. D.
D.
 4. 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 ( )
4. 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 ( )
A. B.
B.
C. D.
D.
5。要得到函数 的图像,只需将函数
的图像,只需将函数 的图像 ( )
的图像 ( )
A.向右平移 个单位
B. 向右平移
个单位
B. 向右平移 个单位
个单位
C. 向左平移 个单位
D. 向左平移
个单位
D. 向左平移 个单位
个单位
6.在正 中,若点
中,若点 分别是
分别是 的中点,则以
的中点,则以 为焦点,且过
为焦点,且过 的双曲线的离心率为
(
)
的双曲线的离心率为
(
)
A. B.
B. C.
C. D.
D.
7.已知直线 交于A、B两点,O是坐标原点,向量
交于A、B两点,O是坐标原点,向量 、
、 满
满
足 ,则实数
,则实数 的值 ( )
的值 ( )
A.2 B.- 或-
或- D.2或-2
D.2或-2
8. 根据表格中的数据,可以断定方程 的一个根所在的区间是
( )
的一个根所在的区间是
( )










…










…










…
(A) (B)
(B) (C)
(C) (D)
(D)
9.在数列 中,如果存在非零常数T,使得
中,如果存在非零常数T,使得 对任意正整数m均成立,那么就称
对任意正整数m均成立,那么就称 为周期数列,其中T叫做数列
为周期数列,其中T叫做数列 的周期。已知数列
的周期。已知数列 满足
满足

 ,且
,且 当数列
当数列 周期为3时,则该数列的前2009项的和为
( )
周期为3时,则该数列的前2009项的和为
( )
A . 1340 B .
10。定义在 上的函数
上的函数 满足
满足 ,当
,当 时,
时, 单调递增,如果
单调递增,如果 ,且
,且 ,则
,则 的值为
( )
的值为
( )
A.恒大于 B. 恒小于
B. 恒小于 C.可能为
C.可能为 D.可正可负
D.可正可负

|
 的值的一个程序框图,其中判断框内应填入的条件是 .
的值的一个程序框图,其中判断框内应填入的条件是 .  对任意实数
对任意实数 .
. 是各项都是正数的等比数列
是各项都是正数的等比数列 的前
的前 项和,若
项和,若 ,则公比
,则公比 和双曲线余弦函数
和双曲线余弦函数 ,而双曲线正弦函数和双曲线余弦函数与我们学过的正弦函数和余弦函数有关类似的性质,比如关于正、余弦函数有
,而双曲线正弦函数和双曲线余弦函数与我们学过的正弦函数和余弦函数有关类似的性质,比如关于正、余弦函数有 成立,而关于双曲正、余弦函数满足
成立,而关于双曲正、余弦函数满足 。请你运用类比的思想,写出关于双曲正弦、双曲余弦很熟的一个新关系式
。请你运用类比的思想,写出关于双曲正弦、双曲余弦很熟的一个新关系式
 的解集是
的解集是 ,则以下结论中:①
,则以下结论中:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ,正确结论的序号是
,正确结论的序号是 
 分别为角A、B、C所对的边,且
分别为角A、B、C所对的边,且
 的周长为L,求L的最大值。
的周长为L,求L的最大值。 中,
中, 面
面 ,
,
 ,
, ,
, ,
, 为
为 的中点。
的中点。 面
面 ;
; 的余弦值
的余弦值
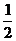
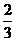

 ,求随机变量
,求随机变量 的中心,焦点与该椭圆的右焦点重合. (Ⅰ)求抛物线D的方程; (Ⅱ)已知动直线
的中心,焦点与该椭圆的右焦点重合. (Ⅰ)求抛物线D的方程; (Ⅱ)已知动直线 过点P(4,0),交抛物线D于A、B两点,坐标原点O为线段PQ中点,求证:
过点P(4,0),交抛物线D于A、B两点,坐标原点O为线段PQ中点,求证: ;(Ⅲ)是否存在垂直于
;(Ⅲ)是否存在垂直于 被以AP为直径的圆所截得的弦长恒为定值?如果存在,求出
被以AP为直径的圆所截得的弦长恒为定值?如果存在,求出 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线
 为
为 ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数). 的极值; (Ⅱ) 函数
的极值; (Ⅱ) 函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由. ,Q=
,Q= ,若矩阵PQ对应的变换把直线
,若矩阵PQ对应的变换把直线 变为直线
变为直线 ,求
,求 的值.
的值. .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: (
( 是参数).
是参数). 参数方程转化为直角坐标普通方程;
参数方程转化为直角坐标普通方程; ,试求实数
,试求实数 值
值 .
(Ⅰ)作出函数
.
(Ⅰ)作出函数 的图象;
的图象; 的解集为
的解集为 ,求
,求 值.
值. 12。12
13。
12。12
13。






 。。。。。。。。。。。。。。。。。。。 4分
。。。。。。。。。。。。。。。。。。。 4分 。。。。。。。。。。。。。。。。。。。 6分
。。。。。。。。。。。。。。。。。。。 6分
 。。。。。。。。。。。。。。。。。。。 8分
。。。。。。。。。。。。。。。。。。。 8分 。。。。。。。。。。。。。。。。。。。. 9分
。。。。。。。。。。。。。。。。。。。. 9分 。。。。。。。。。。。。。。。。。。。. 12分
。。。。。。。。。。。。。。。。。。。. 12分 。。。。。。。。。。。。。。 13分
。。。。。。。。。。。。。。 13分 平面BDC1,OD
平面BDC1,OD 平面BDC1
平面BDC1 所在直线为
所在直线为 轴建立空间直角坐标系 则C1(0,0,3) B(0,2,0) D(1,0,0) C(0,0,0) 。。。。。。。。。。。。。。。。。 8分
轴建立空间直角坐标系 则C1(0,0,3) B(0,2,0) D(1,0,0) C(0,0,0) 。。。。。。。。。。。。。。。。。 8分 的法向量为
的法向量为 由
由 得
得 ,取
,取 , 则
, 则 。。。。。。。。。10分
。。。。。。。。。10分 。。。。。。。。。。。。。。。。。。。 11分
。。。。。。。。。。。。。。。。。。。 11分
 。。。。。。。。。13分
。。。。。。。。。13分 、
、 、
、 。。。。。。。。。。。。2分
。。。。。。。。。。。。2分
 。。。。。。。。。。4分
。。。。。。。。。。4分 ,则
,则




 。。。。。。。。。。。。。。。。。。。。。10分
。。。。。。。。。。。。。。。。。。。。。10分





 。。。。。。。。。。13分
。。。。。。。。。。13分 .
. ,得
,得 .
. 抛物线的焦点为
抛物线的焦点为 ,
, .
. . 。。。。。。。。。。。。。。。。。。。。。。。4分
. 。。。。。。。。。。。。。。。。。。。。。。。4分 由于O为PQ之中点,故当
由于O为PQ之中点,故当 轴时由抛物线的对称性知
轴时由抛物线的对称性知 。。。。。。。。。。。。。。。。。。
。。。。。。。。。。。。。。。。。。
 不垂直
不垂直 轴时,设
轴时,设 ,
,
 ,
,
 ,
, ,
, …
…

 满足题意,则圆心
满足题意,则圆心 ,过M作直线
,过M作直线 的垂线,
的垂线, ,可得,
,可得,
 =
=

 =
=

 时,
时, ,此时直线
,此时直线 被以AP为直径的圆截得的弦长恒为定值
被以AP为直径的圆截得的弦长恒为定值 .…12分
.…12分 满足题意.
……13分
满足题意.
……13分
 ,
,  . 。。。。。。。。。。。。。。。。。。2分
. 。。。。。。。。。。。。。。。。。。2分 时,
时, . 。。。。。。。。。。。。。。。。。。。。。。。。。。3分
. 。。。。。。。。。。。。。。。。。。。。。。。。。。3分 当
当 时,
时, ,此时函数
,此时函数 递减;
递减;  时,
时, ,此时函数
,此时函数 . 。。。。。。。。。。。。。。。。。。6分
. 。。。。。。。。。。。。。。。。。。6分 和
和 的图像在
的图像在 处有公共点,因此若存在
处有公共点,因此若存在 ,则直线方程为
,则直线方程为 ,
, .。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分 ,可得
,可得 当
当 时恒成立.
时恒成立. ,
,  ,得
,得 .。。。。。。。。。。。。。。。。。10分
.。。。。。。。。。。。。。。。。。10分 当
当 时恒成立.
时恒成立.
 ,则
,则 , 。。。。。。。。。。。。。。。。。。。。。。11分
, 。。。。。。。。。。。。。。。。。。。。。。11分 .
. ,此时函数
,此时函数 递增;
递增; ,此时函数
,此时函数 ,即
,即 恒成立.。。。。。。。13分
恒成立.。。。。。。。13分
 .。。。。。。。。。。。。。。。14分
.。。。。。。。。。。。。。。。14分 (当且当
(当且当 ,使得
,使得 和
和 恒成立,
恒成立, 且
且
 ,即
,即 . 。。。。。。。。。。。。。。。。。。。。。。。。8分
. 。。。。。。。。。。。。。。。。。。。。。。。。8分 ,
, 满足条件
满足条件 . 所以
. 所以 。。。。。。。。。。。。。。。。。。(3分)
。。。。。。。。。。。。。。。。。。(3分) 任取点
任取点 ,则点
,则点 在直线
在直线 上,
上, ,又
,又 所以
所以 。。。。。(7分)
。。。。。(7分) 化为直角坐标方程为:
化为直角坐标方程为: 直线
直线 的直角坐标方程为:
的直角坐标方程为: 。。。。。。。。。3分
。。。。。。。。。3分

 或
或 。。。。。。。。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。。。。。。。。7分 (
( 是参数)代入方程
是参数)代入方程 ,
,  .
.



 如图所示。。。。。。。。。。。。。3分
如图所示。。。。。。。。。。。。。3分
 的图象
的图象 .
.  或
或 时,
时, 且
且 即
即
 得:
得:
 。。。。。。。。。。。。。。。。7分
。。。。。。。。。。。。。。。。7分