重庆市丰都中学2009届高三第五次月考
数学(文科)试题
第Ⅰ卷(选择题,共60分)
一.填空题:本大题共12个小题,每小题5分,共60分,在每个小题给出的四个选项中,有且只有一个符合.
1.设集合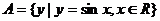 ,那么正确的结论是
,那么正确的结论是
A.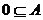 B.
B.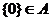 C.
C.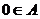 D.
D.
2.下列公式错误的是
A.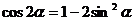 B.
B.
C.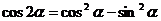 D.
D.
3.已知命题p: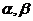 为锐角△ABC的两内角;命题q:
为锐角△ABC的两内角;命题q: 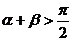 ,则p是q的
,则p是q的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4.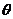 是任意实数,则方程
是任意实数,则方程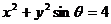 所表示的曲线不可能是
所表示的曲线不可能是
A.椭圆 B.双曲线 C.抛物线 D.圆
5.已知抛物线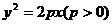 的焦点为F,点
的焦点为F,点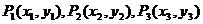 在抛物线上,且
在抛物线上,且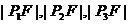 成等差数列,则有
成等差数列,则有
A.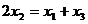 B.
B.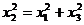 C.
C.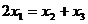 D.
D.
6. 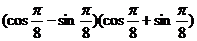 的值为
的值为
A.1 B.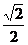 C.
C.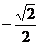 D. -1
D. -1
7.(改编题)正项等比数列 满足
满足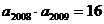 ,则
,则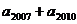 的最小值为
的最小值为
A.16
B.
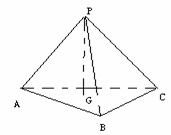 8.(改编题)在三棱锥P-ABC中,G是△ABC内一点,且
8.(改编题)在三棱锥P-ABC中,G是△ABC内一点,且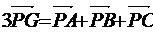 ,则点G是△ABC的
,则点G是△ABC的
A.重心 B.内心
C.垂心 D.外心
9.已知函数f(x) ( 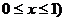 的图像是一段弧若
的图像是一段弧若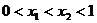 ,则
,则
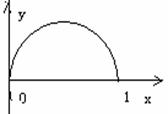 A.
A.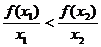 B.
B.
C.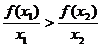 D.
前三个判断都不正确
D.
前三个判断都不正确
10.方程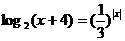 的实根个数为
的实根个数为
A. 1 B.
11.设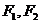 分别是双曲线
分别是双曲线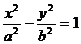 的左.右焦点,P为双曲线上任一点,若
的左.右焦点,P为双曲线上任一点,若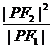 的最小值为
的最小值为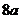 ,则此双曲线的离心率e的取值范围是
,则此双曲线的离心率e的取值范围是
A. 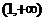 B.
B.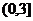 C.
C. 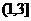 D.
D. 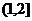
12.对任意正数x,y,不等式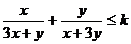 恒成立,则k的取值范围是
恒成立,则k的取值范围是
A.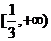 B.
B.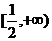 C.
C. 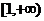 D.
D. 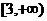
第Ⅱ卷(非选择题,共140分)
二.填空题:本大题共4个小题,每小题4分,共16分.把答案填在题中横线上.
13. 椭圆的长轴长.短轴长.焦距成等比数列,则椭圆的离心率e=
14.已知 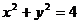 ,则2x+3y的取值范围是
,则2x+3y的取值范围是
15.向量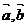 的夹角为
的夹角为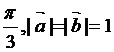 ,则
,则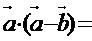
16. 不等式组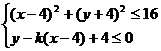 所围成的区域的面积是
所围成的区域的面积是
三.解答题:本大题共6个大题,共74分,解答题应写出文字说明.证明过程或演算步骤。
17.(12分)在△ABC中,角A.B.C所对的边分别是a,b,c,且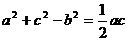
(Ⅰ)求cosB的值;
(Ⅱ)求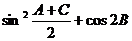 的值。
的值。
18.(12分) (改编题)设函数f(x)=|x-2|+|x+2|。
(Ⅰ)求f(x)的值域;
(Ⅱ)解不等式: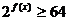 。
。
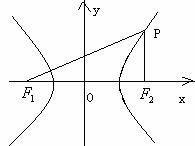 19.(12分)已知
19.(12分)已知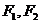 为双曲线
为双曲线 的左右焦点,过
的左右焦点,过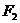 作垂直于x轴的直线交双曲线于点P,且
作垂直于x轴的直线交双曲线于点P,且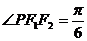 ,求双曲线的离心率和渐近线方程。
,求双曲线的离心率和渐近线方程。
20.(12分)已知函数f(x)= 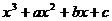 在
在 与x=1时都取得极值,
与x=1时都取得极值,
(Ⅰ)求a,b的值;
(Ⅱ)若对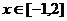 ,不等式
,不等式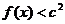 恒成立,求c的取值范围。
恒成立,求c的取值范围。
21.(13分)在数列{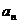 }中,
}中,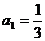 ,并且对任意
,并且对任意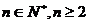 都有
都有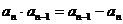 成立,令
成立,令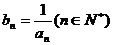
(1)求数列{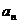 }的通项公式;
}的通项公式;
(2)设数列{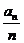 }的前n项和
}的前n项和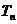 ,求证:
,求证: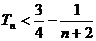 .
.
22.(13分) 如图,椭圆C: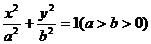 的一个焦点为
的一个焦点为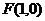 ,点(2,0)在椭圆C上,AB为垂直于x轴的动弦,直线
,点(2,0)在椭圆C上,AB为垂直于x轴的动弦,直线 与x轴交于点N,直线AF与BN交于点M。
与x轴交于点N,直线AF与BN交于点M。
(Ⅰ)求椭圆C的方程;
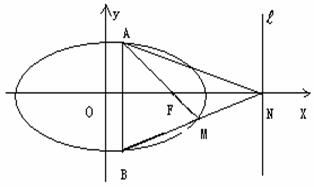 (Ⅱ)求动点M的轨迹方程;
(Ⅱ)求动点M的轨迹方程;
(Ⅲ)猜想△AMN的面积的最大值,并证明你的结论.
选择题(60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D.
A
C
A
B
B
A
C
A
C
B
填空题(16分)
13  14
14  15
15  16 8
16 8
17解:(1)由已知得, ………………6分
………………6分
(2) ………10分
………10分
=- ………12分
………12分
18解:(Ⅰ)(法一)f(x)的定义域为R。

 ,
,
所以f(x)在 上单调递增,在
上单调递增,在 上单调递减。……4分
上单调递减。……4分
所以f(x)值域为 ……6分
……6分
(法二) ……4分
……4分
所以f(x)的值域是 ………6分
………6分
(法三)由绝对值的几何意义知f(x)= 表示数轴上点P(x)到点M(2)与点N(-2)距离之和.……4分
表示数轴上点P(x)到点M(2)与点N(-2)距离之和.……4分
所以f(x)的值域是 .……6分
.……6分
(Ⅱ)原不等式等价于:
① 或②
或② 或③
或③ ……11分
……11分
所以原不等式解集为 ……12分
……12分
 19 解:设
19 解:设 ,由题意知
,由题意知 ,
, ……6分
……6分
又
所以双曲线方程为 ……10分
……10分
所以双曲线的渐近线方程为 ……12分
……12分
20解:(Ⅰ)由题意知方程 的两根是
的两根是
 ……4分
……4分
(Ⅱ)
 在[-1,2]上恒成立,………6分
在[-1,2]上恒成立,………6分
令
 ……8分
……8分
当x在[-1,2]上变化时, 的变化情况如下:
的变化情况如下:
x
-1



1
(1,2)
2

+
-
+
g(x)

ㄊ
极大值

ㄋ
极小值

ㄊ
2
所以当x=2时, ,
,
所以c的取值范围为 ……12分
……12分
21解:(1)当n=1时, ,当
,当 时,由
时,由 得
得 所以
所以 …………4分
…………4分
所以数列 是首项为3,公差为1的等差数列,
是首项为3,公差为1的等差数列,
所以数列 的通项公式为
的通项公式为 …………6分
…………6分
(2)
 22解 :(Ⅰ)由题设a=2,c=1从而
22解 :(Ⅰ)由题设a=2,c=1从而 所以椭圆的方程为:
所以椭圆的方程为:  ………5分
………5分
(Ⅱ)由题意得F(1,0),N(4,0),设A(m,n)
则B(m,-n)( ①
①
设动点M(x,y).AF与BN的方程分别为:n(x-1)-(m-1)y=0 ② n(x-4)+(m-4)y=0 ③
由②③得:当 时,
时, 代入①得
代入①得
当 时,由②③得:
时,由②③得: ,解得n=0,y=0与
,解得n=0,y=0与 矛盾,所以的轨迹方程为
矛盾,所以的轨迹方程为 。…………9分
。…………9分
(Ⅲ)△AMN的面积为△AFN与△MFN面积之和,且有相同的底边FN,当两高之和最大时,面积最大,这时AM应为特殊位置,所以猜想:当AM与x轴垂直时,△AMN的面积最大,|AM|=3,|FN|=3,这时 ,△AMN的面积最大最大值为
,△AMN的面积最大最大值为 ………11分。
………11分。
证明如下:设AM的方程为x=ty+1,代入 得
得
设A ,则有
,则有
令 ,则
,则
因为 ,所以
,所以 ,即
,即 时
时 有最大值3,△AMN的面积有
有最大值3,△AMN的面积有 最大值
最大值 。……13分
。……13分