桓台一中阶段性测试理科数学试题
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项是符合题目要求的,把正确的选项的代号涂在答题卡上。
1、已知复数Z=1+i,则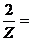
A、-2i B、2i C、1-i D、1+i
2、已知随机变量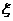 服从正态分布N(3,a
服从正态分布N(3,a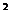 ),
),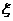 则P(
则P(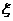 <3)等于
<3)等于
A、 B、
B、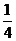 C、
C、 D、
D、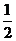
3、已知抛物线x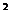 =4ay,则焦点到其准线的距离为
=4ay,则焦点到其准线的距离为
A、a
B、
4、函数 的最小正周期和最大值分别为
的最小正周期和最大值分别为
(A)  ,1
(B)
,1
(B)  ,
,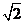 (C)
(C)
 ,1
(D)
,1
(D)  ,
,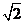
5、若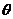 是第二象限的角,则下列四个值中,恒小于零的是
是第二象限的角,则下列四个值中,恒小于零的是
A、sin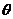 B、sin
B、sin C、cos2
C、cos2 D、tan2
D、tan2
6、已知m,n是两条不同的直线,a,β为两个不同的平面,有下列四个命题:
①、若m⊥a,n⊥β,m⊥n,则a⊥β; ②、若m∥a,n∥β,m⊥n,则a∥β;
③、若m⊥a,n∥β,m⊥n,则a∥β; ④、若m⊥a,n∥β,a∥β,则m⊥n;
其中正确命题的个数为:A、1 B、2 C、3 D、4
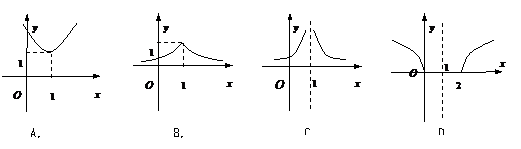 7、若实数
7、若实数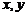 满足
满足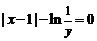 ,则
,则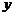 关于
关于 的函数的图象大致是( ).
的函数的图象大致是( ).
8、命题“对任意的 ,
,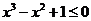 ” 的否定是
” 的否定是
(A)不存在 ,
,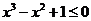 (B) 存在
(B) 存在 ,
,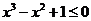
(C) 存在 ,
, (D)
对任意的
(D)
对任意的 ,
,
9、设数列 是首项为1公比为3的等比数列,把
是首项为1公比为3的等比数列,把 中的每一项都减去2后,得到一个新数列
中的每一项都减去2后,得到一个新数列 ,
, 的前n项和为Sn,对任意的n∈N+,下列结论正确的是
的前n项和为Sn,对任意的n∈N+,下列结论正确的是
A、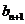 =3
=3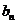 且
且 B、
B、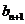 =3
=3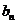 -2且
-2且
C、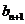 =3
=3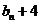 且
且 D、
D、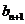 =3
=3 且
且
10、已知平面直角坐标系,xoy中,△OFP面积为2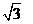 ,且
,且
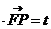 ,设4<t<4
,设4<t<4 ,则向量
,则向量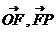 的夹角
的夹角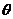 的取值范围是
的取值范围是
A、(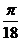 ,
,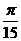 ) B、(
) B、(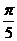 ,
,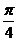 ) C、(
) C、(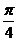 ,
,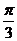 ) D、(
) D、(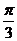 ,
,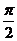 )
)
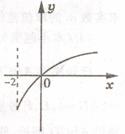 11、已知函数f(x)的定义域是[-2,+∞)且f(4)=f(-2)=1,
11、已知函数f(x)的定义域是[-2,+∞)且f(4)=f(-2)=1,  的导数,且y=
的导数,且y=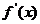 的图象如图所示,则平面区域
的图象如图所示,则平面区域 所围成的面积是
所围成的面积是
A、2 B、4 C、5 D、8
12、位于坐标原点的一个质点 按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是
按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是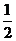 . 质点
. 质点 移动五次后位于点
移动五次后位于点 的概率是
的概率是
(A) 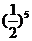 (B)
(B)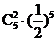 (C)
(C)
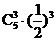 (D)
(D)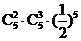
二、填空题:本大题有4个小题,每小题4分,共16分
13、某工厂生产了某种产品6000件,它们来自甲、乙、丙3条生产线,为检查这批产品的质量,决定采用分层抽样的方法进行抽样,若从甲、乙、丙三条生产线抽取的个体数分别为a、b、c,且a、b、c构成等差数列,则乙生产线生产了_____________件产品。
14、若方程lnx-6+2x=0的解为xo,则满足不等式m≤xo的最大整数m是___________。
15、与直线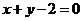 和曲线
和曲线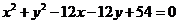 都相切的半径最小的圆的标准方程是__________________。
都相切的半径最小的圆的标准方程是__________________。
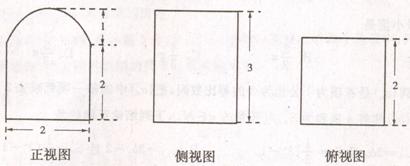 16、已知某个几何体的三视图如图(正视图中弧线为半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积为_____________cm3。
16、已知某个几何体的三视图如图(正视图中弧线为半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积为_____________cm3。
三解答题
17.(本小题满分12分)
已知函数f(x)=2sin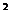 (
(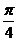 +x)―
+x)― cos2x-1,x ∈R
cos2x-1,x ∈R
(1)求f(x)的最小正周期和单调增区间;
(2)设p: ,q:ㄏf(x)-mㄏ<3,若p是q的充分条件,求实数m的取值范围。
,q:ㄏf(x)-mㄏ<3,若p是q的充分条件,求实数m的取值范围。
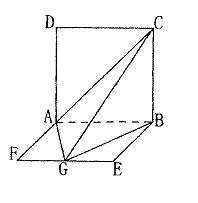 18.(本题满分12分)
18.(本题满分12分)
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 ,G是EF的中点.
,G是EF的中点.
(1)求证平面AGC⊥平面BGC;
(2)求GB与平面AGC所成角正弦值;
19.(本小题满分12分)

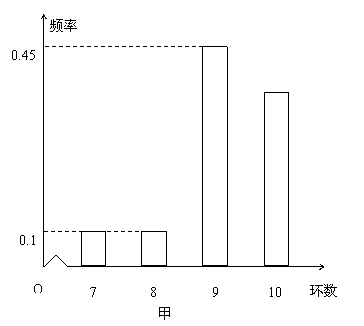 甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.根据以往的统计数据, 甲、乙射击环数的频率分布条形图如下:
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.根据以往的统计数据, 甲、乙射击环数的频率分布条形图如下:
若将频率视为概率,回答下列问题:
(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(Ⅱ)若甲、乙两运动员各自射击1次,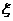 表示这2次射击中击中9环以上(含9环)的次数,求
表示这2次射击中击中9环以上(含9环)的次数,求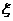 的分布列及数学期望
的分布列及数学期望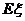 .
.
20(本小题满分12分)
已知函数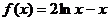 .
.
(Ⅰ)写出函数 的定义域,并求其单调区间;
的定义域,并求其单调区间;
(Ⅱ)已知曲线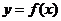 在点
在点 处的切线是
处的切线是 ,求
,求 的值.
的值.
21(本小题满分12分)
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为3,最小值为1.
上的点到焦点距离的最大值为3,最小值为1.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线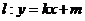 与椭圆
与椭圆 相交于
相交于 两点(
两点( 不是左右顶点),且以
不是左右顶点),且以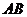 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点. 求证:直线
的右顶点. 求证:直线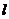 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
一选择题
CDDAB BBCCC BB
二填空题
13、2000 14、2 15、 16、8+π
16、8+π
17解:(1)∵(x)=2sin (
( +x)×
+x)× cos2x-1=1-cos(
cos2x-1=1-cos( +2x)-
+2x)- cos2x-1
cos2x-1
=sin2x- cos2x=2sin(2x-
cos2x=2sin(2x- )…………………3分
)…………………3分
∴T=π……………………………………………………………4分
由2kπ- ≤2x-
≤2x- ≤2kπ得 kπ-
≤2kπ得 kπ- ≤x≤kπ+
≤x≤kπ+ π(k∈Z)
π(k∈Z)
即f(x)单调增区间为[kπ- ,kπ+
,kπ+ ](k∈Z)………………6分
](k∈Z)………………6分
(2)若p成立,即x∈[ ,
, ]时,2x-
]时,2x- ∈[
∈[ ,
, ],f(x)∈[1,2],……8分
],f(x)∈[1,2],……8分
由ㄏf(x)-mㄏ< 3=>m-3<f(x)<m+3………………………………… 9分
∵p是q的充分条件,
∴ m-3<1 m+3>2,解得-1<m<4,即m的取值范围是(-1,4)…………… 12分
18. 解:(Ⅰ)设事件 表示甲运动员射击一次,恰好击中9环以上(含9环),则
表示甲运动员射击一次,恰好击中9环以上(含9环),则
 .
……………….3分
.
……………….3分
甲运动员射击3次均未击中9环以上的概率为
 .
…………………5分
.
…………………5分
所以甲运动员射击3次,至少有1次击中9环以上的概率为
 .
………………6分
.
………………6分
(Ⅱ)记乙运动员射击1次,击中9环以上为事件 ,则
,则
 …………………8分
…………………8分
由已知 的可能取值是0,1,2.
…………………9分
的可能取值是0,1,2.
…………………9分
 ;
;
 ;
;
 .
.
 的分布列为
的分布列为

0
1
2

0.05
0.35
0.6
………………………10分
所以
故所求数学期望为 .
………………………12分
.
………………………12分
19.解法一(几何法)
(1)证明:正方形ABCD ∵面ABCD⊥面ABEF且交于AB,
∵面ABCD⊥面ABEF且交于AB,
∴CB⊥面ABEF ∵AG,GB 面ABEF, ∴CB⊥AG,CB⊥BG
面ABEF, ∴CB⊥AG,CB⊥BG
又AD=2a,AF=a,ABEF是矩形,G是EF的中点,
∴AG=BG= ,AB=2a,AB2=AG2+BG2,∴AG⊥BG ∵CG∩BG=G,
,AB=2a,AB2=AG2+BG2,∴AG⊥BG ∵CG∩BG=G,
∴AG⊥平面CBG 面AG 面AGC, 故平面AGC⊥平面BGC.…4分
面AGC, 故平面AGC⊥平面BGC.…4分
 (2)解:如图,由(Ⅰ)知面AGC⊥面BGC,
(2)解:如图,由(Ⅰ)知面AGC⊥面BGC,
且交于GC,在平面BGC内作BH⊥GC,
垂足为H,则BH⊥平面AGC,
∴∠BGH是GB与平面AGC所成的角
∴Rt△CBG中
又BG= ,∴
,∴ ……8分
……8分
(3)由(Ⅱ)知,BH⊥面AGC, 作BO⊥AC,垂足为O,连结HO,
则HO⊥AC,∴∠BOH为二面角B―AC―G的平面角在Rt△ABC中,
在Rt△BOH中,
即二面角B―AC―G的平面角的正弦值为 .
……12分
.
……12分
[方法二](向量法)
解法:以A为原点,AF所在直线为x轴,AB所在直线为y轴,AD所在直线为z轴建立直角坐标系,
则A(0,0,0),B(0,2a,0),C(0,2a,2a),G(a,a,0),F(a,0,0)
(2)由题意可得 ,
,
 , 设平面AGC的法向量为
, 设平面AGC的法向量为 ,
,
由

(3)因 是平面AGC的法向量,又AF⊥平面ABCD,
是平面AGC的法向量,又AF⊥平面ABCD,
平面ABCD的法向量 , 得
, 得
∴二面角B―AC―G的的平面角的正弦值为 .
.
20. (Ⅰ)函数 的定义域为:
的定义域为: .
…………………………1分
.
…………………………1分
∵ , ∴
, ∴ .
.
令 ,则
,则 .
……………3分
.
……………3分
当 在
在 上变化时,
上变化时, 的变化情况如下表
的变化情况如下表





+
0
-

ㄊ
极大值
ㄋ
∴函数 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 . …………6分
. …………6分
(Ⅱ)由题意可知: ,
…………………7分
,
…………………7分
曲线 在点
在点 处的切线的斜率为
处的切线的斜率为 . …8分
. …8分
∴切线方程为: .
……………9分
.
……………9分
∴ .
.
∴ .
……………10分
.
……………10分
∵切线方程为 , ∴
, ∴ . ∴
. ∴ .
.
∴曲线 在点
在点 处的切线的斜率
处的切线的斜率 . ………12分
. ………12分
21. 解:(1)由题意设椭圆的标准方程为 ,
,
由已知得: ,
,
∴ ,
, ,∴
,∴
∴椭圆的标准方程为
(2)设 、
、 ,
,
联立 得
得

又 ,
,
因为以 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,
,
∴ ,即
,即 .
.
∴
∴
∴
解得:
 ,且均满足
,且均满足 .
.
当 时,
时, 得方程为
得方程为 ,直线过定点(2,0),与已知矛盾;
,直线过定点(2,0),与已知矛盾;
当 时,
时, 得方程为
得方程为 ,直线过定点(
,直线过定点( ,0),
,0),
所以直线 过定点,定点坐标为(
过定点,定点坐标为( ,0).
,0).
22(本小题满分12分)
设Sn是数列 的前n项和,且
的前n项和,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 使
使
 ,求
,求 的通项公式;
的通项公式;
(3)设 ,且数列
,且数列 的前n项和为Tn,试比较Tn与
的前n项和为Tn,试比较Tn与 的大小.
的大小.
解:(1)∵ ,∴
,∴ ,
,
于是an+1=Sn+1-Sn=(2 an+1-2)-(2 an-2),即an+1=2an. …………2分
又a1=S1=2 a1-2, 得a1=2. …………3分
∴ 是首项和公比都是2的等比数列,故an=2n.
…………4分
是首项和公比都是2的等比数列,故an=2n.
…………4分
(2) 由a1b1=(2×1-1)×21+1+2=6及a1=2得b1=3. …………5分
当 时,
时,
 ,
,
∴ .
…………7分
.
…………7分
∵an=2n,∴bn=2n+1( ).
…………8分
).
…………8分
∴ …………10分
…………10分
(3) . …………12分
. …………12分
 .
.
…………14分

