山东省乐陵一中2009届高三考前回扣45分钟练习七
立体几何
一、选择题
1、若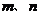 是两条不同的直线,
是两条不同的直线, 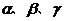 是三个不同的平面,则下列命题中为真命题的是
( )
是三个不同的平面,则下列命题中为真命题的是
( )
A
若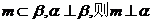 B若
B若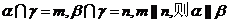
C
若 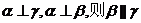 D 若
D 若 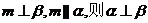
2、已知直线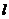 ⊥平面
⊥平面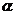 ,直线
,直线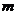
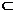 平面
平面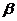 ,下面有三个命题:
,下面有三个命题:
①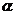 ∥
∥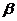
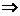
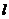 ⊥
⊥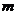 ;②
;②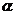 ⊥
⊥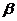
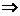
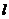 ∥
∥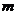 ;③
;③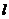 ∥
∥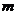
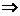
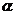 ⊥
⊥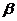 ;
;
则真命题的个数为 ( )
A.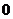 B.
B. 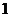 C.
C.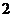 D.
D.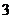
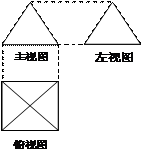
3、如右图,一个简单空间几何体的三视图其主视图与左视图
都是边长为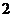 的正三角形,其俯视图轮廓为正方形,则其体积是 ( )
的正三角形,其俯视图轮廓为正方形,则其体积是 ( )
 A.
A.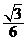 B.
B. 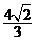 C.
C. 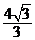 D.
D. 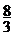
4、已知两条不重合的直线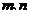 和两个不重合的平面
和两个不重合的平面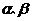 ,有下列命题:
,有下列命题:
①若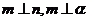 ,则
,则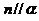 ;②若
;②若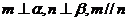 ,则
,则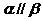 ;
;
③若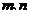 是两条异面直线,
是两条异面直线,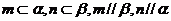 ,则
,则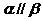 ;
;
④若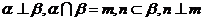 ,则
,则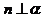 .
.
其中正确命题的个数是 ( )
A.1
B
5、 (09聊城一模)如图是一个几何体的三示图,该几何体的体积是( )
A.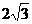 B.
B.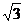 C.
C.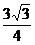 D.
D.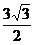

6、设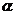 、
、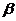 是两个不同的平面,
是两个不同的平面,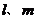 为两条不同的直线,命题p:若平面
为两条不同的直线,命题p:若平面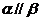 ,
,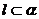 ,
,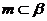 ,则
,则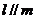 ;命题q:
;命题q: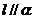 ,
,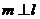 ,
,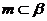 ,则
,则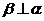 ,则下列命题为真命题的是 ( )
,则下列命题为真命题的是 ( )
A.p或q B.p且q C.┐p或q D.p且┐q
二、填空题
7、一个几何体的三视图如图所示,则这个几何体的体积等于

8、在棱长为2的正方体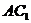 中,G是
中,G是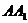 的中点,则
的中点,则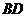 到平面
到平面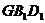 的
的
距离是
9、已知正方体外接球的体积是 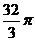 ,则正方体的
,则正方体的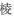 长等于
长等于
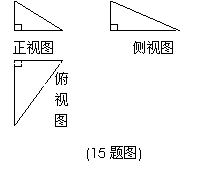
10、某简单几何体的三视图如图所示,其正视图、侧视图、俯视图的面积分别
是1,2,4,则这个几何体的体积为 .
三、解答题
11、 如图所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且PB=PC=
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且PB=PC=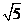 .
.
(Ⅰ)求证:AB⊥CP;
(Ⅱ)求点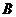 到平面
到平面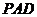 的距离;
的距离;
(Ⅲ)设面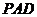 与面
与面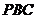 的交线为
的交线为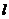 ,求二面
,求二面
角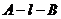 的大小.
的大小.
12、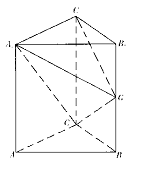 如图,在直棱柱ABC-A1B
如图,在直棱柱ABC-A1B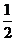 AA1,∠ACB=90º,G为BB1的中点。
AA1,∠ACB=90º,G为BB1的中点。
(I) 求证:平面A1CG⊥平面A1GC1;
(II) 求平面ABC与平面A1GC所成锐二面角的平面角的余弦值。
1、D 2、C 3、C 4、C 5、B 6、C
7、4 8、 9、
9、 10、
10、 
11、解:(Ⅰ) ∵ 底面ABCD是正方形,
∵ 底面ABCD是正方形,
∴AB⊥BC,
又平面PBC⊥底面ABCD
平面PBC ∩ 平面ABCD=BC
∴AB ⊥平面PBC
又PC 平面PBC
平面PBC
∴AB ⊥CP ………………3分
(Ⅱ)解法一:体积法.由题意,面 面
面 ,
,
取 中点
中点 ,则
,则
 面
面 .
.
再取 中点
中点 ,则
,则 ………………5分
………………5分
设点 到平面
到平面 的距离为
的距离为 ,则由
,则由



 .
………………7分
.
………………7分
 解法二:
解法二: 面
面
取 中点
中点 ,再取
,再取 中点
中点

 ,
,


过点 作
作 ,则
,则
在 中,
中,
由
∴点 到平面
到平面 的距离为
的距离为 。 ………………7分
。 ………………7分
(Ⅲ)
 面
面


 就是二面角
就是二面角 的平面角.
的平面角.


∴二面角 的大小为45°. ………………12分
的大小为45°. ………………12分
12、解:(I)证明:在直棱柱ABC-A1B
∵
∠ACB=90º,∴A
∵CG 平面C1CBB1,∴A
平面C1CBB1,∴A
在矩形C1CBB1中,CC1=BB1=2BC,G为BB1的中点,
CG= BC,C
BC,C BC,CC1=2BC
BC,CC1=2BC
∴∠CGC1=90,即CG⊥C
而A
∴CG⊥平面A1GC1。
∴平面A1CG⊥平面A1GC1。┉┉┉┉┉┉┉┉6分
(II)由于CC1平面ABC,
∠ACB=90º,建立如图所示的空间坐标系,设AC=BC=CC1=a,则A(a,0,0),B(0,a,0)
A1(a,0,
∴ =(a,0,
=(a,0, =(0,a,a). ┉┉┉┉┉┉┉┉8分
=(0,a,a). ┉┉┉┉┉┉┉┉8分
设平面A1CG的法向量n1=(x1,y1,z1),
由 得
得
令z1=1,n1=(-2,-1,1). ┉┉┉┉┉┉┉┉9分
又平面ABC的法向量为n2=(0,0,1) ┉┉┉┉┉┉┉┉10分
设平面ABC与平面A1CG所成锐二面角的平面角为θ,
则 ┉┉┉┉┉┉┉┉11分
┉┉┉┉┉┉┉┉11分
即平面ABC与平面A1CG所成锐二面角的平面角的余弦值为 。┉┉┉12分
。┉┉┉12分