2009年安徽省数学高考模拟卷二
第一卷 选择题(共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的
1、 已知全集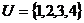 ,集合
,集合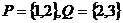 ,则
,则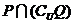 等于
等于
A.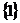 B.
B.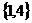 C.
C. D.
D.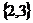
2、已知命题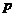 :
: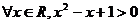 ,则命题┐
,则命题┐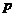 是
是
A. 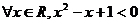 B.
B.
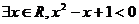
C. 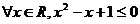 D.
D.
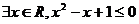
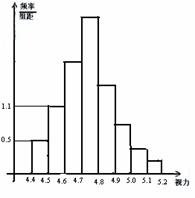 3.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到
3.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道后5组的频数成等比数列,设视力在4.6到 之间的学生数为
之间的学生数为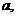 最大频率为
最大频率为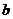 ,则a, b的值分别为( )
,则a, b的值分别为( )
A.77, 0.53 B.70, 0.32
C.77, 5.3 D.70, 3.2
4.设数列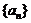 是等差数列,且
是等差数列,且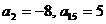 ,
,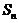 是数列
是数列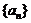 的前
的前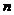 项和,则
项和,则
A.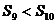 B.
B.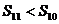 C.
C.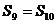 D.
D.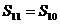
5.设随机变量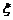 服从标准正态分布
服从标准正态分布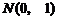 ,在某项测量中,已知
,在某项测量中,已知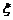 在(-∞,-1.96]内取
在(-∞,-1.96]内取
值的概率为0.025,则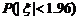 等于
等于
A.0.025 B.
6.过点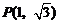 作圆
作圆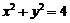 的切线,则切线方程是
的切线,则切线方程是
A.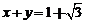 B.
B.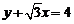
C.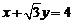 D.
D.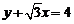 和
和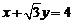
7.掷一个骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数
出现”,则一次试验中,事件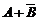 发生概率为
发生概率为
A.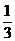 B.
B.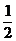 C.
C.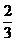 D.
D.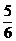
 8.当点
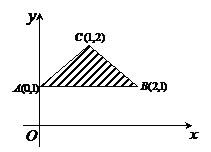
8.当点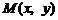 在如图所示的三角形
在如图所示的三角形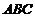 内(含边界)运动时,目标函数
内(含边界)运动时,目标函数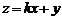 取
取
得最大值的一个最优解为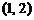 ,则实数
,则实数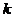 的取值范围是
的取值范围是
A.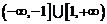
B.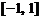
C.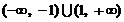
D.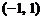
6、函数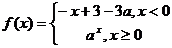 (
(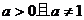 )是
)是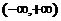 上的减函数,则
上的减函数,则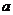 的取值范围是
的取值范围是
A.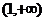 B.
B.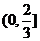 C.
C.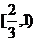 D.
D. 
10.已知双曲线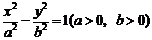 的右顶点为E,双曲线的左准线与该双曲线的两
的右顶点为E,双曲线的左准线与该双曲线的两
渐近线的交点分别为A、B两点,若∠AEB=60°,则该双曲线的离心率e是
A.2
B.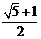 C.
C.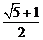 或2
D.不存在
或2
D.不存在
11.已知△ABC中,角A、B、C的对边分别为a、b、c,AH为BC边上的高,以下结论
不正确的是:
A.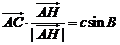 B.
B. 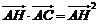
C.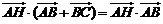 D.
D. 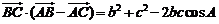
8
3
4
1
5
9
6
7
2
12. 将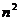 个正整数
个正整数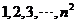 填入
填入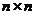 方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做
方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做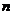 阶幻方.记
阶幻方.记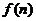 为
为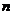 阶幻方对角线上数的和,如右图就是一个
阶幻方对角线上数的和,如右图就是一个
 阶幻方,可知
阶幻方,可知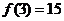 .已知将等差数列:
.已知将等差数列: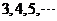 前
前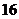 项填入
项填入 方格中,可得到一个
方格中,可得到一个 阶幻方,则其对角线上数的和等于 ( C )
阶幻方,则其对角线上数的和等于 ( C )
A.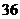 B.
B. C.
C. D.
D.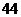
第二卷 非选择题(共90分)
二、填空题:本大题共4小题,每小题4分,共16分.将答案填在题中的横线上
13、已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位: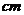 ),可得这个几何体的表面积是
。
),可得这个几何体的表面积是
。


第14题
14.如下图2,是计算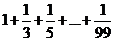 的程序框图,判断框应填的内容是___________,处理框应填的内容是____________.
的程序框图,判断框应填的内容是___________,处理框应填的内容是____________.
15.已知函数 满足对任意
满足对任意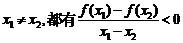
成立,则a的取值范围是 .
16、设函数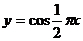 的图象位于
的图象位于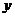 轴右侧所有的对称中心从左依次为
轴右侧所有的对称中心从左依次为 ,则
,则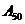 的坐标是
。
的坐标是
。
三、解答题:本大题共6小题,共74分.解答应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知:在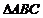 中,
中,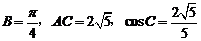 .
.
(Ⅰ)求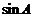 ;
;
(Ⅱ) 记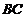 的中点为
的中点为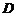 ,求中线
,求中线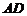 的长.
的长.
|
 . 记
. 记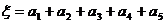 ,当程序运行一次时
,当程序运行一次时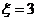 的概率;
的概率; (II)求
(II)求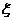 的分布列和数学期望.
的分布列和数学期望. 右焦点
右焦点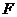 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆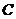 于
于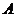 、
、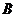 两点,
两点, 为弦的中点;又函数
为弦的中点;又函数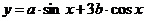 的图像的一条对称轴的方程是
的图像的一条对称轴的方程是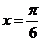 。
。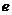 与
与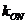 ;
;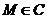 ,试证:总存在角
,试证:总存在角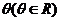 使等式:
使等式: 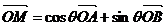 成立.
成立.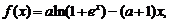 (其中
(其中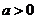 ),点
),点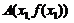 ,
, ,
,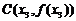 从左到右依次是函数
从左到右依次是函数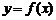 图象上三点,且
图象上三点,且 .
. 上是减函数;
上是减函数;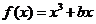 ,数列
,数列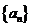 ,其中
,其中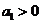 。
。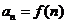 ,当数列
,当数列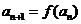 ,当数列
,当数列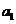 的取值范围
的取值范围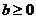 )。
)。 ,
, ;14.
;14.  ;15.
;15.  .16.
.16. 
 ,
,  是三角形内角,得
是三角形内角,得 ……………..
…………….. ………………………………………..
……………………………………….. …………………………………………………………6分
…………………………………………………………6分 中,由正弦定理,
中,由正弦定理, ,
,

 ,
, 
 ………………………………12分
………………………………12分 ,
, …………4分
…………4分 的取值可以是1,2,3,4,5,.
的取值可以是1,2,3,4,5,.
 …………8分
…………8分 的分布列是
的分布列是




 …………12分
…………12分
 .)
.) CD,又AE∥CD,AE=
CD,又AE∥CD,AE= 平面PCE,∴AF∥平面PCE. …………………………………(4分)
平面PCE,∴AF∥平面PCE. …………………………………(4分) 平面PEC,∴面PEC⊥面PCD. 在平面PCD内过F作FH⊥PC于H,则FH就是点F到平面PCE的距离. …………………………………(10分)
平面PEC,∴面PEC⊥面PCD. 在平面PCD内过F作FH⊥PC于H,则FH就是点F到平面PCE的距离. …………………………………(10分) ,PF=
,PF= ,PC=
,PC= ,△PFH∽△PCD,∴
,△PFH∽△PCD,∴ ,
, .
………………………………………………………………(12分)
.
………………………………………………………………(12分)


 =
= +
+ =
= ,∴AF∥EM,又EM
,∴AF∥EM,又EM (2)以A为坐标原点,分别以
(2)以A为坐标原点,分别以 所在直线为x、y、z
所在直线为x、y、z , C(3, 2, 0),
, C(3, 2, 0), =(x, y, z),则
=(x, y, z),则 ,
, ,而
,而 ,0,2),
,0,2), x,z=
x,z= =(0,1,-1),
=(0,1,-1), .…………(12分)
.…………(12分) .又
.又 ,故
,故 为第一象限角,且
为第一象限角,且 .
. 图像的一条对称轴方程式是:
图像的一条对称轴方程式是:  得
得 又
又 c为半点焦距,
c为半点焦距,
 知椭圆C的方程可化为
知椭圆C的方程可化为 (1)
(1) ),AB所在的直线方程为
),AB所在的直线方程为 (2)
(2分)
(2)
(2分) (3)
(3) ),B(
),B( ),弦AB的中点N(
),弦AB的中点N( ),则
),则 是方程(3)的两个不等的实数根,由韦达定理得
是方程(3)的两个不等的实数根,由韦达定理得
 (4)
(4)

 即为所求。
(5分)
即为所求。
(5分) 与
与 是平面内的两个不共线的向量,由平面向量基本定理,对于这一平面内的向量
是平面内的两个不共线的向量,由平面向量基本定理,对于这一平面内的向量 ,有且只有一对实数
,有且只有一对实数 使得等式
使得等式 成立。设
成立。设 由1)中各点的坐标可得:
由1)中各点的坐标可得:

 在椭圆
在椭圆
 (5)
(5) 又
又 两点在椭圆上,故1有
两点在椭圆上,故1有 入(5)式化简得:
入(5)式化简得:
 得到
得到 又
又 是唯一确定的实数,且
是唯一确定的实数,且 ,故存在角
,故存在角 ,使
,使 成立,则有
成立,则有
 ,则存在角
,则存在角 使等式
使等式 成立;若
成立;若 由
由 与
与 于是用
于是用 ,同样证得存在角
,同样证得存在角 ,总存在角
,总存在角

 在
在 上是单调减函数.
上是单调减函数. …………………………4分
…………………………4分 且x1<x2<x3,
且x1<x2<x3, …………………………6分
…………………………6分
 …………………8分
…………………8分

 是钝角三角形……………………………………..9分
是钝角三角形……………………………………..9分 假设ㄓ
假设ㄓ






 ①
…………………………………………
①
………………………………………… ②
② ,故(2)式等号不成立.这与
,故(2)式等号不成立.这与 式矛盾. 所以ㄓ
式矛盾. 所以ㄓ ,又
,又 ,
, 为递增数列即为,
为递增数列即为, 时,
时, 恒成立
恒成立 ,当
,当 时,
时, 的最大值为
的最大值为 。∴
。∴  。∴b的取值范围是:
。∴b的取值范围是: (6分)
(6分) ①又
①又  ②
②
 ,
, 时,有
时,有 成立,
成立, 与
与 同号,于是由递推关系得
同号,于是由递推关系得 同号,因此只要
同号,因此只要 就可推导
就可推导 。又
。又
 ,又
,又
 ,
, 的取值范围是
的取值范围是