广东省梅县华侨中学2008届高三第一次月考试题――数学
2007.8.
一、选择题:(每小题5分, 共50分)
1.设集合A=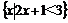 ,B=
,B=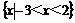 ,则
,则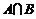 等于( )
等于( )
A 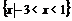 B
B
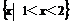 C{x | x>-3} D {x | x<1}
C{x | x>-3} D {x | x<1}
2.已知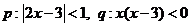 , 则
, 则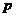 是
是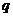 的(
)条件.
的(
)条件.
A. 充分不必要 B. 必要不充分 C. 充要 D. 既不充分也不必要
3.设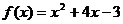 ,则
,则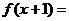 ( )
( )
A.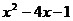 B.
B.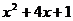 C.
C. 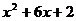 D.
D.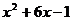
4. 函数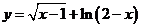 的定义域是
的定义域是
(A)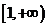 (B)
(B)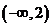 (C)
(C)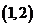 (D)
(D)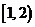
5. 下列函数中,在其定义域内既是奇函数又是减函数的是( )
A. 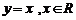 B.
B. 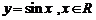 C.
C. 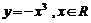 D.
D. 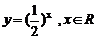
6. 有下列四个命题:
①“若x+y=0 , 则x ,y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤1 ,则x2 + 2x+q=0有实根”的逆否命题;
④“不等边三角形的三个内角相等”逆命题;
其中真命题为 ( )
A.①② B.②③ C.①③ D.③④
7. 已知点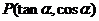 在第三象限, 则角
在第三象限, 则角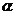 的终边在(
).
的终边在(
).
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
8. 若函数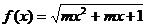 的定义域是
的定义域是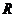 ,则
,则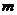 的取值范围是( )
的取值范围是( )
A.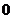 <
<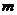 <
<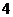 B.
B.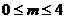 C.
C.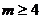 D.
D.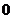 <
<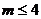
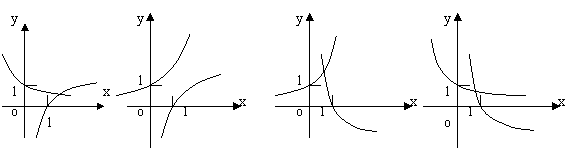 9. 10)当
9. 10)当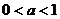 时,在同一坐标系中,函数
时,在同一坐标系中,函数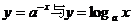 的图象是( )
的图象是( )
A B C D
10. 设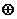 是
是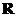 上的一个运算,
上的一个运算,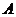 是
是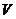 的非空子集,若对任意
的非空子集,若对任意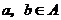 ,有
,有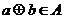 ,则称
,则称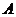 对运算
对运算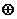 封闭.下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )
封闭.下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是( )
A.自然数集 B.有理数集 C.整数集 D.无理数集
二、填空题(每题5分,共20分)
11.若幂函数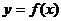 过点
过点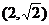 ,则
,则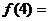
12. 设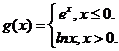 则
则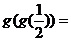 __________.
__________.
13. 如果奇函数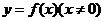 在
在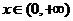 时,
时, 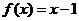 , 则
, 则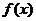 在整个定义域上的解析式为
.
在整个定义域上的解析式为
.
14. 已知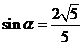 ,
,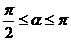 ,则
,则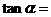
三、解答题:本大题共6小题,共80分,解答应写出文字说明、演算步骤或推证过程。
15.(本小题满分12分)
已知函数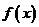 在定义域
在定义域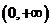 上为增函数,且满足
上为增函数,且满足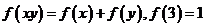
(1)求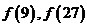 的值
(2)解不等式
的值
(2)解不等式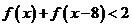
16.(本题12分)已知函数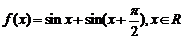 .
.
(1)求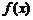 的最小正周期;
的最小正周期;
(2)若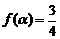 ,求
,求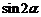 的值.
的值.
17.(本小题满分14分)
已知函数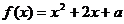 ,
,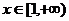
①当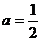 时,求函数
时,求函数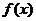 的最小值。
的最小值。
②若对任意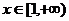 ,
,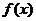 >
>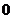 恒成立,试求实数
恒成立,试求实数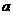 的取值范围。
的取值范围。
18.(本小题满分14分)
已知函数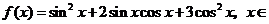
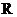 ,
,
求(1)函数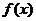 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量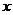 的集合;
的集合;
(2)函数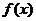 的单调增区间.
的单调增区间.
19. (本小题满分14分)
一个小服装厂生产某种风衣,月销售量x(件)与售价P(元/件)之间的关系为P=160-2x,生产x件的成本R=500+30x元
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
20. (本小题满分14分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点 已知函数f(x)=ax2+(b+1)x+(b?1)(a≠0)
已知函数f(x)=ax2+(b+1)x+(b?1)(a≠0)
(1)若a=1,b=?2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
广东省梅县华侨中学2008届高三第一次月考试题――数学
2007.8.
答题卡
班级 姓名 座号 成绩
题号
1
2
3
4
5
6
7
8
9
10
答案
11 ;12 ;
13 ;14 .
三、解答题:本大题共6小题,共80分,解答应写出文字说明、演算步骤或推证过程。
15.(本小题满分12分)
已知函数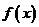 在定义域
在定义域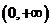 上为增函数,且满足
上为增函数,且满足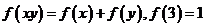
(1)求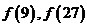 的值
(2)解不等式
的值
(2)解不等式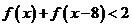
16.(本题12分)已知函数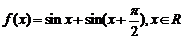 .
.
(1)求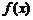 的最小正周期;
的最小正周期;
(2)若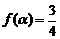 ,求
,求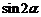 的值.
的值.
17.(本小题满分14分)已知函数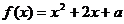 ,
,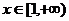
①当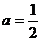 时,求函数
时,求函数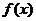 的最小值。
的最小值。
②若对任意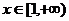 ,
,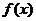 >
>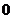 恒成立,试求实数
恒成立,试求实数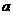 的取值范围。
的取值范围。
18.(本小题满分14分)已知函数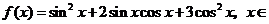
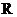 ,
,
求(1)函数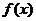 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量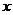 的集合;
的集合;
(2)函数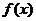 的单调增区间.
的单调增区间.
19. (本小题满分14分)
一个小服装厂生产某种风衣,月销售量x(件)与售价P(元/件)之间的关系为P=160-2x,生产x件的成本R=500+30x元
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
20. (本小题满分14分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点 已知函数f(x)=ax2+(b+1)x+(b?1)(a≠0)
已知函数f(x)=ax2+(b+1)x+(b?1)(a≠0)
(1)若a=1,b=?2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
广东省梅县华侨中学2008届高三第一次月考试题――数学
一、选择题:(每小题5分, 共50分)
1――
二、填空题(每题5分,共20分)
11. 2 12. 
13.  14.
14.  -2
-2
三、解答题:本大题共6小题,共80分,解答应写出文字说明、演算步骤或推证过程。
15.(本小题满分12分)
解:(1)
(2)
而函数f(x)是定义在 上为增函数
上为增函数

即原不等式的解集为
16. 解: ….4分
….4分
(1) 的最小正周期为
的最小正周期为 ;。。。。8分
;。。。。8分
(2)因为 ,即
,即 ,即
,即  。。。。12分
。。。。12分
17. (1)当 有最小值为
有最小值为 。…….7分
。…….7分
(2)当 ,使函数
,使函数 恒成立时,故
恒成立时,故 。。。。14分
。。。。14分
18. (I)解法一:


 ……4分
……4分
 当
当 ,即
,即 时,
时, 取得最大值
取得最大值
因此, 取得最大值的自变量x的集合是
取得最大值的自变量x的集合是 .……8分
.……8分
解法二:

 ……4分
……4分
 当
当 ,即
,即 时,
时, 取得最大值
取得最大值 .
.
因此, 取得最大值的自变量x的集合是
取得最大值的自变量x的集合是 ……8分
……8分
(Ⅱ)解:
由题意得 ,即
,即 .
.
因此, 的单调增区间是
的单调增区间是 .…………12分
.…………12分
19. 解 (1)设该厂的月获利为y,依题意得?。。。。2分
(1)设该厂的月获利为y,依题意得?。。。。2分
y=(160-2x)x-(500+30x)=-2x2+130x-500。。。。。4分
由y≥1300知-2x2+130x-500≥1300
∴x2-65x+900≤0,∴(x-20)(x-45)≤0,解得20≤x≤45。。。。6分
∴当月产量在20~45件之间时,月获利不少于1300元 。。。。。。7分
。。。。。。7分
(2)由(1)知y=-2x2+130x-500=-2(x- )2+1612
)2+1612 5。。。。。。9分
5。。。。。。9分
∵x为正整数,∴x=32或33时,y取得最大值为1612元,。。。12分
∴当月产量为32件或33件时,可获得最大利润1612元 。。。。。14分
。。。。。14分
20. 解 (1)当a=1,b=?2时,f(x)=x2?x?3,。。。。2分
(1)当a=1,b=?2时,f(x)=x2?x?3,。。。。2分
由题意可知x=x2?x?3,得x1=?1,x2=3 。。。。6分
。。。。6分
故当a=1,b=?2时,f(x)的两个不动点为?1,3 。。。。7分
。。。。7分
(2)∵f(x)=ax2+(b+1)x+(b?1)(a≠0)恒有两个不动点,
∴x=ax2+(b+1)x+(b?1),
即ax2+bx+(b?1)=0恒有两相异实根。。。。。9分
∴Δ=b2?4ab+ 。。。。。11分
。。。。。11分
于是Δ′=(
故当b∈R,f(x)恒有两个相异的不动点时,0<a<1 。。。。。。14分
。。。。。。14分